(成都)(本小题满分10分)已知AC,EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90.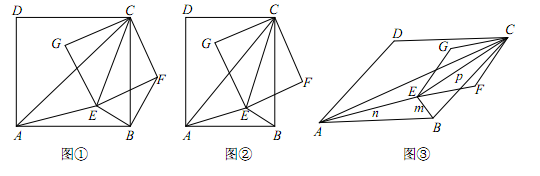
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且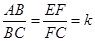 时,若BE=1,AE=2,CE=3,求k的值;
时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.求证:△EBC≌△FDA.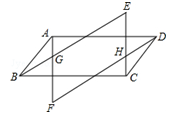
(1)解不等式组: .
.
(2)计算: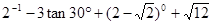
分解因式: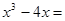 .
.
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.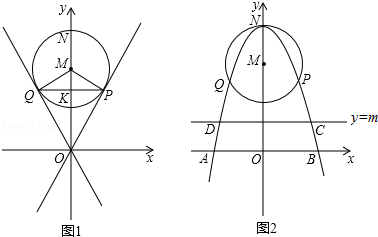
(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
某公司投资700万元购买甲、乙两种产品的生产技术和设备后,进行这两种产品的生产加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价定在35元到70元之间较为合理,设甲种产品的销售单价为x(元),年销售量为y(万件).当35≤x≤50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x之间的函数关系如图所示.乙种产品的销售单价在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.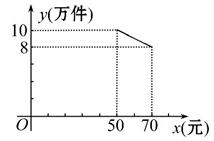
(1)当50≤x≤70时,求出甲种产品的年销售量y(万件)与x(元)之间的函数解析式.
(2)若该公司第一年的年销售利润(年销售利润=年销售收入-生产成本)为W(万元),那么怎样定价,可使第一年的年销售利润最大?最大年销售利润是多少?
(3)第二年公司可重新对产品进行定价,在(2)的条件下,并要求甲种产品的销售单价x(元)在50≤x≤70范围内,该公司希望到第二年年底,两年的总盈利(总盈利=两年的年销售利润之和-投资成本)不低于85万元.请求出第二年乙种产品的销售单价m(元)的范围.