(广安)为了贯彻落实市委市府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A、B两贫困村的计划.现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=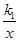 (x>0) 的图象上,点C在反比例函数L2:y=
(x>0) 的图象上,点C在反比例函数L2:y=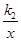 (x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为.(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为.(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=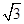 .
.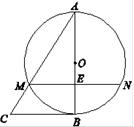
(1)求证:BC是⊙O的切线;
(2)求 的长.
的长.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.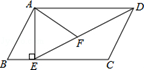
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6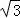 ,AF=4
,AF=4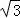 ,求AE的长.
,求AE的长.
热气球C从建筑物A的底部沿直线开始斜着往上飞行,当飞行了180米距离时到达如图中的位置,此时在热气球上测得两建筑物A,B底部的俯角分别为30°和60°﹒若此时热气球在地面的正投影D与点A,B在同一直线上.
(1)求此时热气球离地面的高度CD的长;
(2)求建筑物A、B之间的距离(结果中保留根号).