（成都）（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线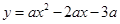
（
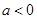）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：
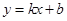与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．
（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；
（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为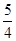
，求a的值；
（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．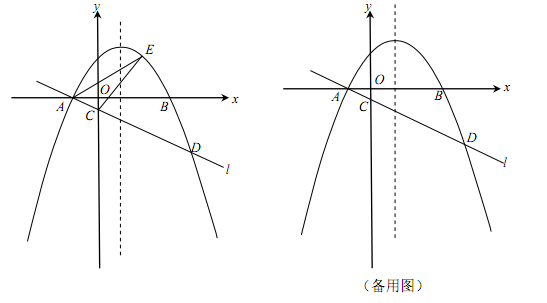
已知抛物线y＝﹣x2+2x+3与x轴交于A，B两点（点A在点B的左侧）．
（1）求点A，点B的坐标；
（2）如图，过点A的直线l：y＝﹣x﹣1与抛物线的另一个交点为C，点P为抛物线对称轴上的一点，连接PA，PC，设点P的纵坐标为m，当PA＝PC时，求m的值；
（3）将线段AB先向右平移1个单位长度，再向上平移5个单位长度，得到线段MN，若抛物线y＝a（﹣x2+2x+3）（a≠0）与线段MN只有一个交点，请直接写出a的取值范围．
如图，在 中， ，以AC为直径作⊙O交BC于点D，过点D作 ，垂足为E，延长BA交⊙O于点F．
（1）求证：DE是⊙O的切线；
（2）若 ， ，求 的半径．
打油茶是广西少数民族特有的一种民俗．某特产公司近期销售一种盒装油茶，每盒的成本价为50元，经市场调研发现，该种油茶的月销售量y（盒）与销售单价x（元）之间的函数图象如图所示．
（1）求y与x的函数解析式，并写出自变量x的取值范围；
（2）当销售单价定为多少元时，该种油茶的月销售利润最大？求出最大利润．
综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
芒果树叶的长宽比 |
3.8 |
3.7 |
3.5 |
3.4 |
3.8 |
4.0 |
3.6 |
4.0 |
3.6 |
4.0 |
|
荔枝树叶的长宽比 |
2.0 |
2.0 |
2.0 |
2.4 |
1.8 |
1.9 |
1.8 |
2.0 |
1.3 |
1.9 |
【实践探究】分析数据如下：
|
平均数 |
中位数 |
众数 |
方差 |
|
|
芒果树叶的长宽比 |
3.74 |
m |
4.0 |
0.0424 |
|
荔枝树叶的长宽比 |
1.91 |
1.95 |
n |
0.0669 |
【问题解决】
（1）上述表格中：m＝ ，n＝ ；
（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”
②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”
上面两位同学的说法中，合理的是 （填序号）；
（3）现有一片长11cm，宽5.6cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．
如图，在 中，BD是它的一条对角线．
（1）求证： ；
（2）尺规作图：作BD的垂直平分线EF，分别交AD，BC于点E，F（不写作法，保留作图痕迹）；
（3）连接BE，若 ，求 的度数．
