（凉山州）在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．
（1）用树状图或列表法列举点M所有可能的坐标；
（2）求点M（x，y）在函数
的图象上的概率；
（3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M（x，y）能作⊙O的切线的概率．
如图3个全等的菱形构成的活动衣帽架，顶点A、E、F、C、G、H是上、下两排挂钩，根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动)，若菱形的边长为16厘米，要使两排挂钩之间 的距离为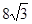
厘米，并在点B、M处固定，则B、M之间的距离是多少？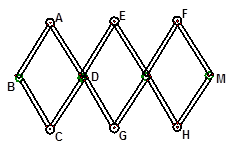
已知：如图，点B、F、C、E在同一直线上，BF=CE，AB⊥BE，DE⊥BE，垂足分别为B、E且AB=DE，连接AC、DF．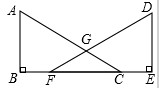
求证：∠A=∠D．
求不等式组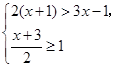
的整数解．
计算或化简：
（1）
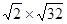
（2）
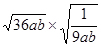
（3）
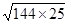
（4）在直角△ABC中，∠C=90
，AC="2" cm ,BC="4" cm ,求AB的长.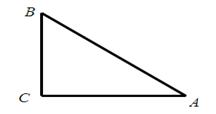
阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣。
当A、B两点中有一点在原点时，不妨设点A在原点，
如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；
当A、B两点都不在原点时，
如图2，点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣；
如图3，点A、B都在原点的左边，
∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=－b-（-a）=∣a-b∣；
如图4，点A、B在原点的两边，
∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣=" a" +（-b）=∣a-b∣；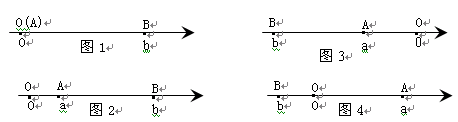
回答下列问题：
（1）数轴上表示2和5的两点之间的距离是_________,数轴上表示－2和－5的两点之间的距离是_________,数轴上表示1和－3的两点之间的距离是_______；
（2）数轴上表示x和－1的两点A和B之间的距离是___________,如果∣AB∣＝2，那么x为____________；
（3）当代数式∣x+1∣＝∣x-2∣取最小值时，相应的x的取值范围是.