已知E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．
试探究下列问题：
（1）如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）
（2）如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；
（3）如图3，在（2）的基础上，连接AE和BF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．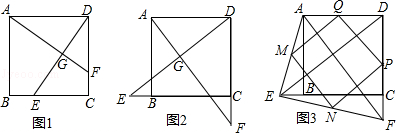
（本题满分12分，其中第（1）小题5分，第（2）小题7分）
已知：如图，在△ABC中，AD是边BC上的中线，点E在线段BD上，且BE=ED，过点B作BF∥AC，交线段AE的延长线于点F．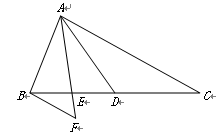
（1）求证：AC=3BF；
（2）如果
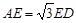，求证：
．
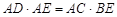（本题满分12分，其中第（1）小题5分，第（2）小题7分）
已知：如图，斜坡AP的坡度为1∶2.4，坡长AP为26米，在坡顶A处的同一水平面上有一座古塔BC，在斜坡底P处测得该塔的塔顶B的仰角为45°，在坡顶A处测得该塔的塔顶B的仰角为76°．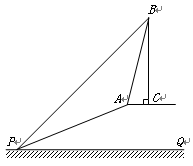
求：（1）坡顶A到地面PQ的距离；
（2）古塔BC的高度（结果精确到1米）．
（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）
已知：如图，矩形DEFG的一边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，AH是边BC上的高，AH与GF相交于点K，已知BC=12，AH=6，EF∶GF=1∶2，求矩形DEFG的周长．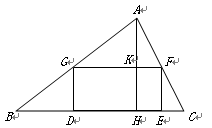
（本题满分10分，其中每小题各5分）
已知：如图，在△ABC中，AB=6，BC=8，∠B=60°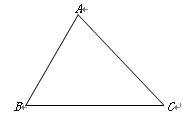
求：（1）△ABC的面积；
（2）∠C的余弦值．
（本题满分10分，其中第（1）小题6分，第（2）小题4分）
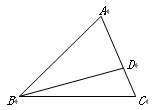
如图，已知在△ABC中，点D在边AC上，CD∶AD=1∶2，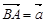
，
．
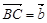（1）试用向量
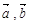表示向量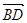
；（2）求作：
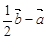．（不要求写作法，但要指出所作
图中表示结论的向量）