(南充)已知抛物线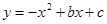 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
(1)求抛物线解析式.
(2)直线 (
(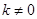 )与抛物线相交于两点M(
)与抛物线相交于两点M(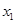 ,
, ),N(
),N( ,
,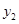 )(
)( ),当
),当 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.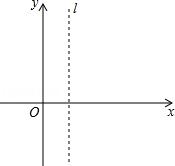
(本题4分)如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至A′的位置,使点A与A′对应,得到△A′B′C′;
(2)线段AA′与BB′的关系是:;
(3)求△ABC的面积.
解下列方程组(每小题3分,共6分)
(1)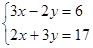
(2) 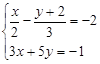
分解因式(每小题3分,共6分)
(1)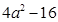
(2)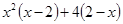
计算(每小题3分,共6分)
(1)
(2)
【阅读理解】对于任意正实数a、b,因为 ≥0,所以
≥0,所以
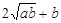 ≥0,所以
≥0,所以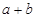 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
【获得结论】在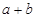 ≥2
≥2 (a、b均为正实数)中,若ab为定值p,则
(a、b均为正实数)中,若ab为定值p,则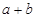 ≥2
≥2 ,只有当a=b时,
,只有当a=b时,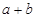 有最小值2
有最小值2 .
.
根据上述内容,回答下列问题:若 >0,只有当
>0,只有当 =时,
=时, +
+ 有最小值.
有最小值.
【探索应用】如图,已知A(-3,0),B(0,-4),P为 双曲线 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D。求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D。求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.