(凉山州)阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF=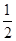 (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点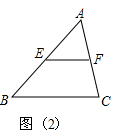
请你运用所学知识,结合上述材料,解答下列问题.
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD=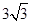 ,OC=5,求MN的长.
,OC=5,求MN的长.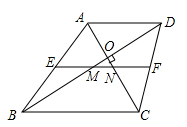
如图,在矩形ABCD中,点O在对角线AC上,以OA长为半径的 与AD,AC分别交于点E,F,∠ACB="∠DCE" .
与AD,AC分别交于点E,F,∠ACB="∠DCE" .
请判断直线CE与
 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;若 DE:EC=1:
 ,
, ,求⊙O的半径.
,求⊙O的半径.
如图,在平行四边形 中,
中, ,
,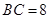 ,
,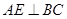 于点
于点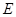 ,
,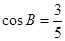 ,求
,求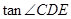 的值.
的值.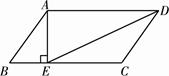
在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分布表和扇形统计图:
根据上述信息回答下列问题:a=,b=;
在扇形统计图中,B组所占圆心角的度数为;
全校共有1000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?
如图,在平面直角坐标系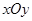 中,直线AB与反比例函数
中,直线AB与反比例函数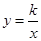 的图像交于点A(-3,4),AC⊥
的图像交于点A(-3,4),AC⊥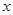 轴于点C.
轴于点C.求此反比例函数的解析式;
当直线AB绕着点A转动时,与
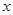 轴的交点为B(a,0),并与反比例函数
轴的交点为B(a,0),并与反比例函数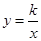 图象的另一支还有一个交点的情形下,求△ABC的面积S与
图象的另一支还有一个交点的情形下,求△ABC的面积S与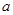 之间的函数关系式.并写出自变量
之间的函数关系式.并写出自变量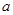 的取值范围.
的取值范围.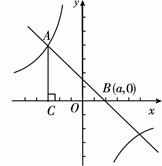
列方程或方程组解应用题:
小明家有一块长8m、宽6m的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的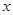 值.
值.