（·衢州市 第24题 12分）如图，在△ABC中，AB=5，AC=9，S△ABC=
，动点P从A点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．
（1）求tanA的值；
（2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；
（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．
如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形.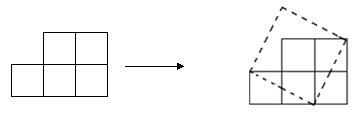
(1)拼成的正方形的面积与边长分别是多少？
(2)你能在3×3方格图中，连接四个点组成面积为5的正方形吗？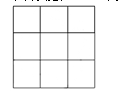
(3)你能把十个小正方形组成的图形纸，剪开并拼成正方形吗?若能，请在图中画出图形，并求出它的边长是多少？ 若不能请说明理由.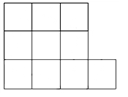
全球气候变暖导致－些冰川融化并消失，在冰川|消失12年后，一种低等植物苔藓，就开始在岩石上生长，每一个苔藓都会长成近似的圆形，苔藓的直径和其生长年限近似地满足如下的关系式：d=7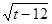
(t≥12)，其中d表示苔藓的直径，单位是厘米，t代表冰川消失的时间(单位：年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米，问冰川约是在多少年前消失的?
为体现社会对教师的尊重，教师节这一天上午，出租车司机小聪在东西方向的公路上免费接送老师.如果规定向东为正，向西为负，出租车的行程如下（单位：千米）：＋15，－4，＋13，―10，―12，＋3,―13,―17.
（1）出车地记为0，最后一名老师送到目的地时，小聪距出车地点的距离是多少？
（2）若汽车耗油量为0.1升/千米，这天上午汽车共耗油多少升？
小刚与小明两位同学利用温差法去测量某座山峰的高度，他们于同一时刻测得山顶温度为-4.2℃，山脚的温度为2.4℃，已知该地区山峰的高度每增加100米，气温大约降低0.6℃，问这座山峰的高度大约是多少米？
在数轴上近似地表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接。
4，－1.5， 0， 
，－π