（·温州卷 第24题 14分）如图，点A和动点P在直线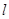
上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O。点C在点P右侧，PC=4，过点C作直线
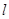⊥，过点O作OD⊥于点D，交AB右侧的圆弧于点E。在射线CD上取点F，使DF=
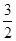CD，以DE，DF为邻边作矩形DEGF，设AQ=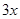
（1）用关于
的代数式表示BQ，DF；
（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长；
（3）在点P的整个运动过程中，
①当AP为何值时，矩形DEGF是正方形？
②作直线BG交⊙O于另一点N，若BN的弦心距为1，求AP的长（直接写出答案）
如图，已知一次函数
的图象与反比例函数
的图象交于
，
两点，且点的横坐标和点的纵坐标都是
．
求：（1）一次函数解析式；
（2）求
的面积．
如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A1B1C1和△A2B2C2；
（1）先作△ABC关于直线成轴对称的图形，再向上平移1个单位，得到△A1B1C1；
（2）以图中的O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△ A2B2C2．
如图，已知抛物线
的对称轴为直线
，交
轴于A、B两点，交
轴于C点，其中B点的坐标为（3，0）．
（1）直接写出A点的坐标；
（2）求二次函数的解析式．
已知二次函数y=-x2+4x+5，完成下列各题：
（1）将函数关系式用配方法化为
的形式，并写出它的顶点坐标、对称轴．
（2）求出它的图象与坐标轴的交点坐标．
（3）在直角坐标系中，画出它的图象．
（4）根据图象说明：当x为何值时，y>0；当x为何值时，y<0．
如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上，AB+BD与DE的长度有什么关系?并加以证明．