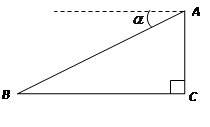(为方便答题,可在答题卡上画出你认为必要的图形)
在Rt△ABC中,∠A=90°,AC =" AB" = 4,D,E分别是边AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰RtRt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
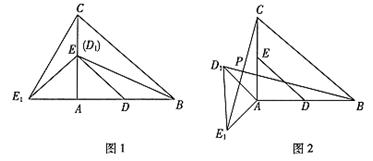
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1 = CE1 ,且BD1⊥ CE1 ;
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)
已知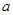 、
、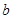 互为相反数,
互为相反数,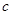 、
、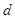 互为倒数,
互为倒数,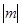 =2,求代数式
=2,求代数式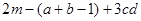 的值。
的值。
某天早上,一辆交通巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,如果规定向东行驶为正,向西行驶为负,行驶纪录如下。(单位:km)
(1)B地在A地哪个方向,与A地相距多少千米?
(2)巡逻车在巡逻过程中,离开A地最远是多少千米?
(3)若每km耗油0.3升,问共耗油多少升?
计算。
(1)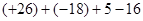
(2)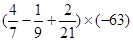
(3)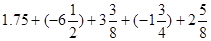
(4)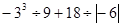
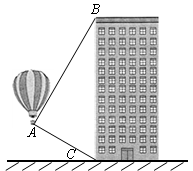
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为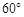 ,看这栋高楼底部的俯角为
,看这栋高楼底部的俯角为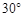 ,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据:
,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据: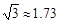 )
)
如图,某飞机于空中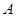 处探测到地平面目标
处探测到地平面目标 ,此时从飞机上看目标
,此时从飞机上看目标 的俯角为
的俯角为 ,若测得飞机到目标
,若测得飞机到目标 的距离
的距离 约为2400米,已知
约为2400米,已知 ,求飞机飞行的高度
,求飞机飞行的高度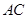 约为多少米?
约为多少米?