在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称之为“理想点”,例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有有无数多个.
(1)若点M(2,a)是反比例函数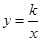 (k为常数,
(k为常数, )图象上的“理想点”,求这个反比例函数的表达式;
)图象上的“理想点”,求这个反比例函数的表达式;
(2)函数 (m为常数,
(m为常数,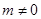 )的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
)的图象上存在“理想点”吗?若存在,请求出“理想点”的坐标;若不存在,请说明理由.
解方程:
(1)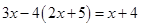 ;
;
(2)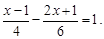
(1)化简:2a-[a-2(a-b)]-b
(2)先化简,再求值:已知多项式A=3 2—6ab+b2,B=—2
2—6ab+b2,B=—2 2+3ab—5b2,当
2+3ab—5b2,当 =1,b=—1时,求A+2B的值.
=1,b=—1时,求A+2B的值.
【问题背景】如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置,然后再证明△AFE ≌△AFG,从而得出结论:___________________.
【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
【结论应用】如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏东60°的A处,舰艇乙在指挥中心南偏西20°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正南方向以40海里/小时的速度前进,舰艇乙沿南偏东40°的方向以50海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
已知:如图1,射线MN⊥AB,AM=1cm,MB=4cm.点C从M出发以2cm/s的 速度沿射线MN运动,设点 C的运动时间为t(s)
(1)当△ABC为等腰三角形时,求t的值;
(2)当△ABC为直角三角形时,求t的值;
(3)当t满足条件:__________时,△ABC为钝角三角形; 当_________时,△ABC为锐角三角形.
爱动脑筋的小明在学习了全等三角形和等腰三角形有关知识后作了如下探索:
(1)已知,如图,△ABC中,∠BAC是锐角,AB=AC,高AD、BG 所在的直线相交于点H, 且AG=BG,则AH和BC的关系是:_____________________;

(2)若把(1)中的“∠BAC是锐角”改为“∠BAC是钝角”(如图2),其他条件都不变, AH和BC的关系是否仍然成立, 若成立,请在图2中用三角板和量角器画出完整的图形并证明;若不成立,请说明理由.