如图,在▱ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表
|
活动次数 |
频数 |
频率 |
|
|
10 |
0.20 |
|
|
|
0.24 |
|
|
16 |
0.32 |
|
|
6 |
0.12 |
|
|
|
|
|
|
2 |
|
根据以上图表信息,解答下列问题:
(1)表中 , ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?

如图, ,以点 为圆心,1为半径画 与 的延长线交于点 ,过点 画 的垂线,垂线与 的一个交点为 ,连接
(1)线段 的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线 交于点 ,使线段 的长等于
②连 ,在 上画出点 ,使 的长等于 ,请写出画法,并说明理由.

一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
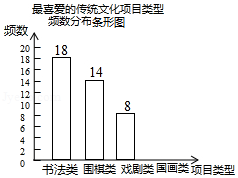
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
|
项目类型 |
频数 |
频率 |
|
书法类 |
18 |
|
|
围棋类 |
14 |
0.28 |
|
喜剧类 |
8 |
0.16 |
|
国画类 |
|
0.20 |
根据以上信息完成下列问题:
(1)直接写出频数分布表中 的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同.
(1)若先从袋子中拿走 个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,则 的值为 ;
(2)若将袋子中的球搅匀后随机摸出1个球(不放回),再从袋中余下的3个球中随机摸出1个球,求两次摸到的球颜色相同的概率.