如图,已知点D在双曲线 (
(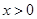 )的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线
)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线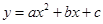 经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.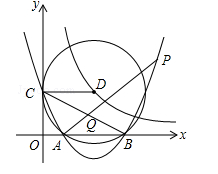
(1)写出点D的坐标并求出抛物线的解析式;
(2)证明∠ACO=∠OBC;
(3)探究是否存在点P,使点Q为线段AP的四等分点?若存在,求出点P的坐标;若不存在,请说明理由.
若 >0,
>0, <0,
<0, >
> ,用“<”号连接
,用“<”号连接 ,
, ,
, ,-
,- ,请结合数轴解答.
,请结合数轴解答.
已知: ,
, ,且
,且 ,求
,求 的值.
的值.
如图,点 是菱形
是菱形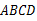 的对角线
的对角线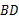 上一点,连接
上一点,连接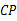 并延长,交
并延长,交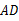 于
于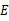 ,交
,交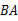 的延长线于点
的延长线于点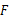 .
.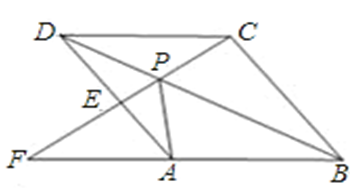
(1)图中△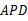 与哪个三角形全等?并说明理由.
与哪个三角形全等?并说明理由.
(2)求证:△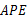 ∽△
∽△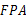 .
.
(3)猜想:线段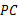 ,
,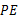 ,
,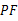 之间存在什么关系?并说明理由.
之间存在什么关系?并说明理由.
已知关于 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
.
(1)求实数 的取值范围;
的取值范围;
(2)当 时,求
时,求 的值.
的值.
如图,在等腰梯形 中,
中, ∥
∥ ,点
,点 是线段
是线段 上的一个动点(
上的一个动点( 与
与 、
、 不重
不重
合), 分别是
分别是 的中点.
的中点.
(1)试探索四边形 的形状,并说明理由.
的形状,并说明理由.
(2)当点 运动到什么位置时,四边形
运动到什么位置时,四边形 是菱形?并加以证明.
是菱形?并加以证明.
(3)若(2)中的菱形 是正方形,请探索线段
是正方形,请探索线段 与线段
与线段 的关系,并证明你的结论.
的关系,并证明你的结论.