抛物线 ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.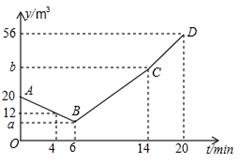

(1)每个出水口每分钟出水 m3,表格中a= ;
(2)求进水口每分钟的进水量和b的值;
(3)在整个过程中t为何值时,水池有水16m3
如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支架底端与桌面顶端的距离OA=75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)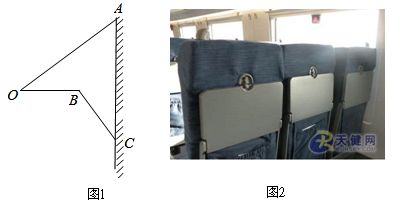
已知P(-5,m)和Q(3,m)是二次函数y=2x2+bx+1图象上的两点.
(1)求b的值;
(2)将二次函数y=2x2+bx+1的图象沿y轴向上平移k(k>0)个单位,使平移后的图象与x轴无交点,求k的取值范围.
.国家环保局统一规定,空气质量分为5级.当空气污染指数达0-50时为1级,质量为优;51-100时为2级,质量为良;101-200时为3级,轻度污染;201-300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题: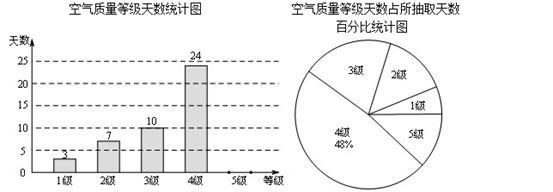
(1)本次调查共抽取了 天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为 °;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)