（来宾）在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．
（1）求证：△CMN∽△BAM；
（2）设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；
（3）当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．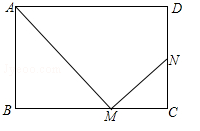
如图，在矩形
中，
是
边上一点，
的延长线交
的延长线于点
，
⊥
，垂足为
，且
．
（1）求证：
；
（2）根据条件请在图中找出一对全等三角形，并证明你的结论．
作一直线，将下图分成面积相等的两部分（保留作图痕迹）．
如图，四边形ABCD是平行四边形，
，BD⊥AD，求BC，CD及OB的长.
某中学为了了解全校的耗电情况，抽查了10天中全校每天的耗电量，数据如下表：
| 千瓦时 |
90 |
93 |
102 |
113 |
114 |
120 |
| 天数 |
1 |
1 |
2 |
3 |
1 |
2 |
（1）写出上表中数据的众数和平均数．
（2）根据上题获得的数据，估计该校一个月的耗电量（按30天计算）．
（3）若当地每千瓦时电的价格是0．5元，写出该校应付电费y（元）与天数
（取正整数，单位：天）的函数关系式．
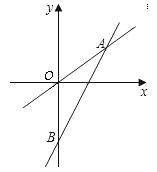
如图表示一个正比例函数与一个一次函数的图象，它们交于点A（4，3），一次函数的图象与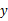
轴交于点B，且OA=OB，求这两个函数的关系式及两直线与
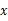轴围成的三角形的面积. 