(南宁)如图,AB是⊙O的直径,C,G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线.
(2)若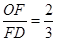 ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ,求AD的长.
,求AD的长.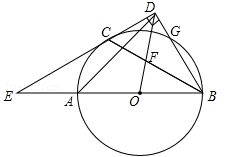
试确定实数a的取值范围,使不等式组 恰有两个整数解.
恰有两个整数解.
(本题满分9分)将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.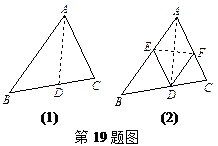
(本题满分8分)已知a=2+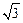 ,b=2-
,b=2-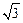 ,试求
,试求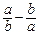 的值.
的值.
8分)已知:关于x 的一元二次方程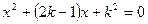 的两根
的两根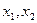 满足
满足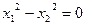 ,双曲线
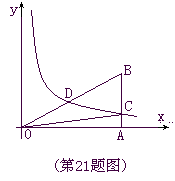
,双曲线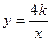 (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),求
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),求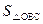 .
.
2010年,世博会在我国的上海举行,在网上随机调取了5月份中的某10天持票入园参观的人数,绘成下面的统计图.根据图中的信息回答下列问题: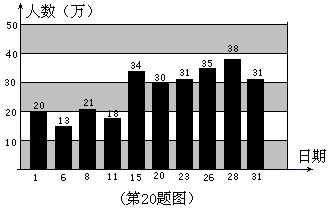
(1)求出这10天持票入园人数的平均数、中位数和众数;
(2)不考虑其它因素的影响,以这10天的数据作为样本,估计在世博会开馆的184天中,持票入园人数超过30万人的有多少天?