(钦州)如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.
(1)求证:BC是⊙O的切线;
(2)连接OC,如果OC恰好经过弦BD的中点E,且tanC=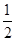 ,AD=3,求直径AB的长.
,AD=3,求直径AB的长.
下图是一个长方体纸盒的展开图,请把-5,3,5,-1,-3,1分别填入六个长方形,使得按虚线折成长方体后,相对面上的两数互为相反数.
写出大于-4.1小于2.5的所有整数,并把它们在数轴上表示出来..
(本小题满分8分)某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
⑴请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
⑵求自变量x的取值范围;
⑶怎样安排生产每天获得的利润最大,最大利润是多少?
(本小题满分8分)星期天,小明与小刚骑自行车去距家
50千米的某地旅游,匀速行驶1.5小时的时候,其中一
辆自行车出故障,因此二人在自行车修理点修车,用了
半个小时,然后以原速继续前行,行驶1小时到达目的
地.请在右面的平面直角坐标系中,画出符合他们行驶
的路程S(千米)与行驶时间t(时)之间的函数图象.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。 求证:⑴△ABC≌△DEF;
求证:⑴△ABC≌△DEF;
⑵GF=GC。