(黔西南州)如图,在平面直角坐标系中,平行四边形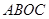 如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形
如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形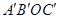 .抛物线
.抛物线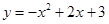 经过点A、C、A′三点.
经过点A、C、A′三点.
(1)求A、A′、C三点的坐标;
(2)求平行四边形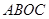 和平行四边形
和平行四边形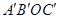 重叠部分
重叠部分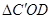 的面积;
的面积;
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,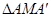 的面积最大?最大面积是多少?并写出此时M的坐标.
的面积最大?最大面积是多少?并写出此时M的坐标.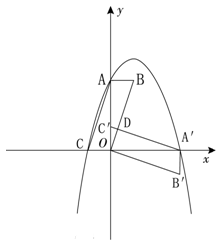
(柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
(南宁)如图,AB是⊙O的直径,C,G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线.
(2)若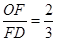 ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ,求AD的长.
,求AD的长.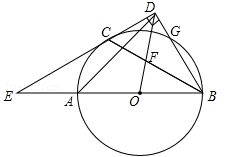
(南宁)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).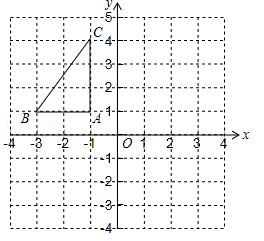
(贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.
(1)求证:AF=EF;
(2)求证:BF平分∠ABD.
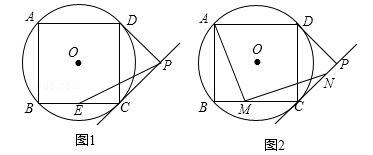
(桂林)如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.