(年蒙自市初中学业水平第一次模拟测试)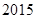 年
年 月
月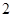 日云南临沧沧源发生
日云南临沧沧源发生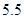 级地震,牵动着全国人民的心,地震后某中学举行了爱心捐款活动,下图是该校九年级某班学生为沧源灾区捐款情况绘制的不完整的条形统计图和扇形统计图.
级地震,牵动着全国人民的心,地震后某中学举行了爱心捐款活动,下图是该校九年级某班学生为沧源灾区捐款情况绘制的不完整的条形统计图和扇形统计图.
(1)求该班人数;
(2)补全条形统计图;
(3)在扇形统计图中,捐款“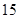 元人数”所在扇形的圆心角的度数;
元人数”所在扇形的圆心角的度数;
(4)若该校九年级有 人,据此样本,请你估计该校九年级学生共捐款多少元?
人,据此样本,请你估计该校九年级学生共捐款多少元?
如图,在平面直角坐标系中,一次函数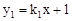 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数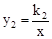 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围。
时x的取值范围。
某商品的进价为每件50元,售价为每件60元,每个月可卖出200件。如果每
件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元)。设每件商品的售价上涨x元(x
为整数),每个月的销售利润为y元,
(1)求y与x的函数关系式,并直接写出x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O
上一点,且∠AED=45°。
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6cm,AE=10cm,求∠ADE的正弦值。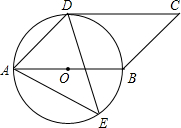
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,
∠E=30°,∠A=45°,AC=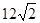 ,试求CD的长。
,试求CD的长。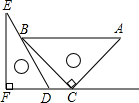
我市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四
个品种的树苗共500株进行树苗成活率试验,从中选取成活率高的品种进行推广。通过实验得知:丙种树
苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出)。
(1)实验所用的乙种树苗的数量是__________株;
(2)求出丙种树苗的成活数,并把图2补充完整;
(3)你认为应选哪一种树苗进行推广?请通过计算说明理由。