(本小题满分10分)选修4—4:参数方程选讲
极坐标系与直角坐标系 有相同的长度单位,以原点
有相同的长度单位,以原点 为极点,以
为极点,以 轴正半轴为极轴.已知曲线
轴正半轴为极轴.已知曲线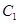 的极坐标方程为
的极坐标方程为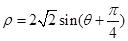 ,曲线
,曲线 的参数方程为
的参数方程为
 为参数,
为参数,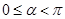 ;射线
;射线 ,
, ,
,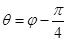 ,
, 与曲线
与曲线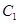 分别交异于极点
分别交异于极点 的四点
的四点 ,
, ,
, ,
, .
.
(1)若曲线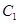 关于曲线
关于曲线 对称,求
对称,求 的值,并把曲线
的值,并把曲线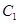 和
和 化成直角坐标方程;
化成直角坐标方程;
(2)求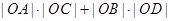 的值.
的值.
已知数列{an}的各项均为正数,观察如图所示的程序框图,若k=5,k=10时,分别有S=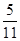 和S=
和S=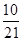 ,求数列{an}的通项公式.
,求数列{an}的通项公式.
在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如下表:
| 场次i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 得分xi |
100 |
104 |
98 |
105 |
97 |
96 |
100 |
为了对这个队的情况进行分析,此人设计计算σ的算法流程图如图所示(其中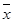 是这7场比赛的平均得分),求输出的σ的值.
是这7场比赛的平均得分),求输出的σ的值.
在可行域内任取一点,规则如流程图所示,求输出数对(x,y)的概率.
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(1)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(≥73公斤)的职工,求体重为76公斤的职工被抽取到的概率.
某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间[40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的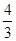 倍.
倍.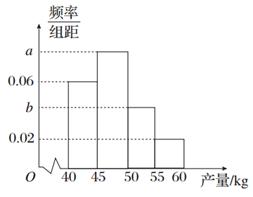
(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树中随机抽取2株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.