跳伞运动是当前比较流行挑战极限的运动之一,尤其是低空跳伞,其危险性比高空跳伞还要高,由于距离有限,打开伞包的时间一般只有几秒钟,很难在空中调整姿势和动作.跳伞运动员到达地面时的安全速度v0=4m/s.若跳伞运动员H=476m高空离开飞机,做自由下落,下落一段高度h1后才打开伞,开伞后以2m/s2的加速度匀减速竖直下落,到达地面恰好达到安全速度v0.(取g=10m/s2),求:
(1)运动员到达地面时安全速度相当于他从多高处h0自由下落?
(2)在空中自由下落的距离h1?
(3)运动员离开飞机后,经过多长时间才能到达地面?
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静时细线AB水平,细线AC与竖直方向的夹角θ=37º。已知小球的质量m=1kg,细线AC长L=1m,B点距C点的水平和竖直距离相等。(重力加速度g取10m/s2,sin37º=0.6,cos37º=0.8)
(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为0,求此时角速度ω2的大小;
(3)装置可以以不同的角速度匀速转动,试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω2变化的关系图像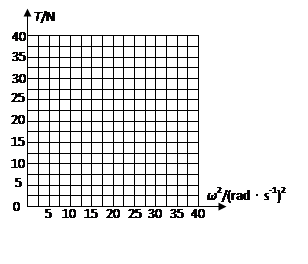
如图所示,ABC为一固定的半圆形轨道,轨道半径R=0.4m,A、C两点在同一水平面上.现从A点正上方h=2m的地方以v0=4m/s的初速度竖直向下抛出一质量m=2kg的小球(可视为质点),小球刚好从A点进入半圆轨道.不计空气阻力,重力加速度g取10 m/s2 .
(1)若轨道光滑,求小球下落到最低点B时的速度大小;
(2)若轨道光滑,求小球相对C点上升的最大高度;
(3)实际发现小球从C点飞出后相对C点上升的最大高度为 2.5m,求小球在半圆轨道上克服摩擦力所做的功.
2.5m,求小球在半圆轨道上克服摩擦力所做的功.
额定功率为P=80kw的汽车,在某平直的公路上行驶,经过时间t=15s速度达到最大为vm=20m/s,汽车的质量m=2×103kg。如果汽车从静止开始做匀加速直线运动,加速度大小为a=2m/s2,运动过程中阻力不变。
求:(1)汽车所受的恒定阻力f;
(2)匀加速运动的时间t1;
(3)3s末汽车的瞬时功率P3;
(4)在15s内汽车运动的总路S。
高空遥感探测卫星在距地球表面高为2R处绕地球转动。人造卫星质量为m,地球半径为R,地球表面重力加速度为g,
试求:(1)人造卫星的运行速度大小v;
(2)人造卫星绕地球转动的周期T;
(3)人造卫星的向心加速度an。
为了探测X星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为r1的圆轨道上运动,周期为T1,总质量为m1。随后登陆舱脱离飞船,变轨登陆X星球。则:
A.X星球的质量为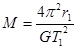 |
| B.当登陆舱脱离飞船后,飞船的运行速度不会发生变化 |
| C.研究人员在飞船内无法用弹簧测力计测量物体的重力,是因为物体不受力的作用 |
| D.登陆舱脱离飞船,变轨后想登陆X星球,登陆舱必须立即减速 |