某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用12万元，以后每年都增加4万元，每年捕鱼收益50万元．
（1）问第几年开始获利？
（2）若干年后，有两种处理方案：①年平均获利最大时，以26万元出售该渔船；②总纯收入获利最大时，以8万元出售该渔船．问哪种方案最合算？
(本小题满分10分)
某单位建造一间地面面积为12m2的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x不得超过
米，房屋正面的造价为400元/m2,房屋侧面
的造价为150元
/m2，屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用．
（1）把房屋总造价
表示成
的函数，并写出该函数的定义域.
（2）当侧面的长度为多少时，总造价最底？最低总造价是多少？
(本小题满分10分)
已知函数
的图像在点
处的切线为
。
（1）求函数
及单调区间；
（2）求函数在区间
上的最值。
（本小题满分10分）
在△ABC中，角A、B、C的对边分别为
、
、
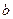.已知
，=
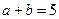，且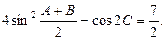
(1) 求角C的大小；（2）求△ABC的面积.
(12分) (2010·黄冈模拟)已知函数f(x)＝()x，x∈[－1,1]，函数g(x)＝f2(x)－2af(x)＋3的最小值为h(a).
(1)求h(a)的解析式；
(2)是否存在实数m，n同时满足下列两个条件：①m>n>3；②当h(a)的定义域为[n，m]时，值域为[n2，m2]？若存在，求出m，n的值；若不存在，请说明理由.
(12分)已知函数f(x)＝(x≠a，a为非零常数)．
(1)解不等式f(x)<x；
(2)设x>a时，f(x)的最小值为6，求a的值。