如图所示,在水平面上放置的相距为0.2m的平行金属导轨与电源、电键、导体棒AB、滑动变阻器可构成闭合电路,磁感应强度为B=0.5T的匀强磁场竖直向下,导体棒AB的质量m=0.5kg,它与轨道之间的动摩擦因数μ=0.05。当电键S闭合时,电路中电流为5A(g取10m/s2).求: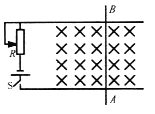
(1)此时导体棒AB受到的安培力大小及方向.
(2)此时导体棒AB的加速度大小.
【改编】如图所示,一根长0.1m的细线,一端系着一个质量为0.2kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动.已知绳能承受的最大拉力为18N,当小球的转速增大为原来的3被时,细线将恰好会断开,求: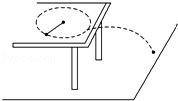
(1)原来绳上的拉力?
(1)线断开的瞬间,小球运动的线速度?
(3)线断开后,小球离开桌面,若桌面高出地面0.8m,求小球飞出后的落地时的速度大小?(取g=10m/s2)
我国的“探月工程”计划将在2017年宇航员登上月球.若宇航员登上月球后,以初速度v0竖直向上拋出一小球,测出小球从抛出到落回原处所需的时间为t 。已知万有引力常量为G、月球的半径为 R ,不考虑月球自转的影响,求:
(1)求月球表面的重力加速度大小g月;
(2)月球的质量M ;
(3)飞船贴近月球表面绕月球做匀速圆周运动的周期T 。
一人用一根长L=1m,最大只能承受T=46N拉力的轻绳子,拴着一个质量m=1kg的小球(不考虑其大小),在竖直平面内作圆周运动,已知圆心O离地高H=21m,如图所示,若小球运动到达最低点时绳刚好被球拉断,(g=10m/s2)求:
(1)小球到达最低点的速度大小是多少?
(2)小球落地点到O点的水平距离是多少?
如图所示,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100 m,子弹射出的水平速度v=200 m/s,子弹从枪口射出的瞬间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10 m/s2,求:
(1)从子弹由枪口射出开始计时,经多长时间子弹击中目标靶?
(2)目标靶由静止开始释放到被子弹击中,下落的距离h为多少?
过山车是游乐场中常见的设施。下图是一种过山车运行轨道的简易模型,它由竖直平面内粗糙斜面轨道和光滑圆形轨道组成。过山车与斜面轨道间的动摩擦因数为 ,圆形轨道半径为R,A点是圆形轨道与斜面轨道的切点。过山车(可视为质点)从倾角为
,圆形轨道半径为R,A点是圆形轨道与斜面轨道的切点。过山车(可视为质点)从倾角为 的斜面轨道某一点由静止开始释放并顺利通过圆形轨道。若整个过程中,人能承受过山车对他的作用力不超过其自身重力的8倍。求过山车释放点距A点的距离范围。
的斜面轨道某一点由静止开始释放并顺利通过圆形轨道。若整个过程中,人能承受过山车对他的作用力不超过其自身重力的8倍。求过山车释放点距A点的距离范围。