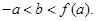如图,直线 平面
平面 ,
, 为正方形,
为正方形, ,求直线
,求直线 与
与 所成角的大小.
所成角的大小.
已知函数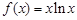 。
。
(I)求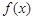 的最小值;
的最小值;
(II)若对所有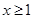 都有
都有 ,求实数
,求实数 的取值范围。
的取值范围。
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=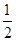 PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q-BP-C的余弦值.
已知函数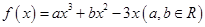 在点
在点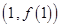 处的切线方程为
处的切线方程为 .
.
⑴求函数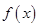 的解析式;
的解析式;
⑵若对于区间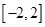 上任意两个自变量的值
上任意两个自变量的值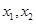 都有
都有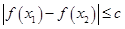 ,求实数
,求实数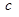 的最小值;
的最小值;
如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,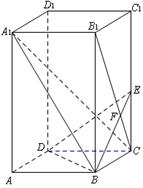
⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
已知函数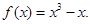
(I)求曲线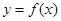 在
在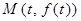 处的切线方程。
处的切线方程。
(II)设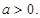 如果过点
如果过点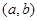 可作曲线
可作曲线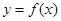 的三条切线,证明:
的三条切线,证明: