如图所示，在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场：垂直纸面向外的匀强磁场I、垂直纸面向里的匀强磁场II，O、M、P、Q为磁场边界和x轴的交点OM=MP=L．在第三象限存在沿y轴正向的匀强电场．一质量为m、带电荷量为+q的粒子从电场中坐标为（﹣2L，﹣L）的点以速度υ0沿+x方向射出，恰好经过原点O处射入区域I又从M点射出区域I（粒子的重力忽略不计）．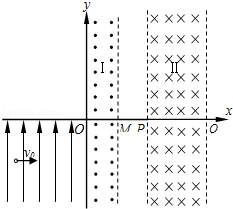
（1）求第三象限匀强电场场强E的大小；
（2）求区域I内匀强磁场磁感应强度B的大小；
（3）如带电粒子能再次回到原点O，问区域II内磁场的宽度至少为多少？粒子两次经过原点O的时间间隔为多少？
如图所示，水平绝缘光滑轨道AB与处于竖直平面内的圆弧形v绝缘光滑轨道BCD平滑连接，圆弧形轨道的半径R=0.30m。轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×107 N/C。现有一电荷量q=-4.0×10-7C，质量m=0.30 kg的带电体（可视为质点），在水平轨道上的P点以某一水平初速度v0向右运动，若带电体恰好可以沿圆弧轨道运动到D点，并在离开D点后，落回到水平面上的P点。，已知OD与OC的夹角θ=37°，求：
（1）P、B两点间的距离x；
（2）带电体经过C点时对轨道的压力；
（3）小球的初速度v0的值。
宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行.设每个星体的质量均为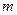
.
（1）试求第一种形式下，星体运动的线速度和周期.
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？
如图所示，一轻绳上端系在车的左上角的A点，另一轻绳一端系在车左端B点，B点在A点正下方，A、B距离为b，两绳另一端在C点相结并系一质量为m的小球，绳AC长度为
，绳BC长度为b。两绳能够承受的最大拉力均为2mg。求：
(1)绳BC刚好被拉直时，车的加速度是多大?
(2)为不拉断轻绳，车向左运动的最大加速度是多大?
（要求画出受力图）
要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道。求摩托车在直道上行驶所用的最短时间.有关数据见表格。
| 启动加速度大小a1 |
4 m/s2 |
| 制动加速度大小a2 |
8 m/s2 |
| 直道最大速度v1 |
40 m/s |
| 弯道最大速度v2 |
20 m/s |
| 直道长度 s |
218 m |
注：制动加速度为匀减速时的加速度
某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1="40" m/s，
然后再减速到v2="20" m/s，t1=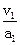
=…；t2=
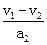=…；t=t1+t2
你认为这位同学的解法是否合理?若合理,请完成计算；若不合理,请说明理由,并用你自己的方法算出正确结果。
一些同学乘坐动车组列车外出旅游,当列车在一段平直轨道上匀加速行驶时,一同学提议说:“我们能否用身边的器材测出列车的加速度?”许多同学参与了测量工作,测量过程如下:他们一边看着窗外铁轨旁边的电线杆,一边用手表记录着时间,已知铁轨旁边每隔100m恰好有一个电线杆，电线杆到铁轨的距离都相等。他们观测到从第一根电线杆运动到第二根电线杆的时间间隔为5s,从第一根电线杆运动到第三根电线杆的时间间隔为9s,请你根据他们的测量情况,求:（计算结果保留2位小数）
（1）列车的加速度大小；
（2）他们运动到第三根电线杆时列车的速度大小.