已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1)若m=4,求直线l被圆C所截得弦长的最大值;
(2)若直线l是圆心下方的切线,当a在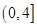 的变化时,求m的取值范围.
的变化时,求m的取值范围.
设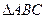 的三条边为
的三条边为 求证
求证
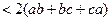 .
.
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为 2m的进出口,
2m的进出口, 如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度
如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度 为
为 (单位:元)。
(单位:元)。
(1)将总造价 表示为
表示为 的函数:
的函数:
(2)试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
已知条件 条件
条件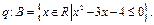 若
若 是
是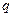 的充分但不必要条件,求实
的充分但不必要条件,求实 数
数 的取值范围.
的取值范围.
某种产品的广告费用支出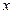 万元与销售额
万元与销售额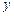 万元之间有如下的对应
万元之间有如下的对应 数据:
数据:
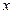 |
2 |
4 |
5 |
6 |
8 |
 |
20 |
30 |
50 |
50 |
70 |
(1)画出上表数据的散点图;
(2)根据上表提供的数据, 求出y关于x的线性回归方程;
求出y关于x的线性回归方程;
(3)据此估计广告费用为10万元时,所得的销售收入.
(参考数值: 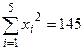 ,
, ,)
,)
(14)已知函数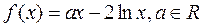
(Ⅰ)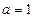 时,求函数
时,求函数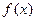 的极值;
的极值;
(Ⅱ)求
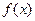 单调区间
单调区间
(Ⅲ)设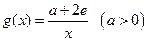 ,若在
,若在 上至少存在一个
上至少存在一个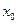 ,使得
,使得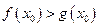 成立,求实数
成立,求实数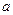 的取值范围。
的取值范围。