如图,在菱形 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, ,在菱形
,在菱形 的外部以
的外部以 为边作等边三角形
为边作等边三角形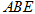 。点
。点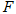 是对角线
是对角线 上一动点(点
上一动点(点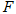 不与点
不与点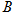 、D重合),将线段
、D重合),将线段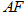 绕点
绕点 顺时针方向旋转
顺时针方向旋转 得到线段
得到线段 ,连接
,连接 。
。
(1)求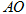 的长;
的长;
(2)如图2,当点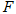 在线段
在线段 上,且点
上,且点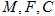 三点在同一条直线上时,求证:
三点在同一条直线上时,求证: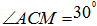
(3)连接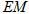 ,若
,若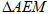 的面积为40,请画出图形,并直接写出
的面积为40,请画出图形,并直接写出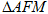 的周长。
的周长。
解方程(本题8分)
(1)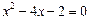 (2)
(2)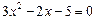
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴子点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1)设点P的纵坐标为p,写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于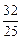 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据某市交通部门统计,2008年底全市汽车拥有量为50万辆,而截止到2010年底,全市 的汽车拥有量已达72万辆.
的汽车拥有量已达72万辆.
(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;
(2)为保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过77.32万辆;另据估计,从2011年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%.假定每年新增汽车数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆.
在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
( 1)求证:△ABD为等腰三角形;
1)求证:△ABD为等腰三角形;
(2)求证:AC·AF=DF·FE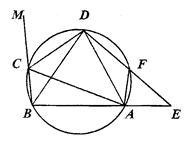
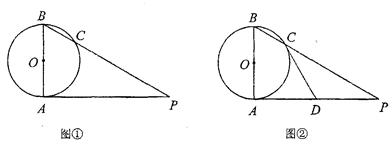
已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若AP=6,PC=4,求圆的半径(结果保留根号);
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.