某超市经销一种成本为40元/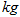 的水产品,市场调查发现,按50元/
的水产品,市场调查发现,按50元/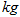 销售,一个月能售出500
销售,一个月能售出500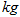 ,销售单价每涨1元,月销售量就减少10
,销售单价每涨1元,月销售量就减少10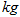 ,针对这种水产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元,请你帮忙算算,销售单价定为多少?
,针对这种水产品的销售情况,超市在月成本不超过10000元的情况下,使得月销售利润达到8000元,请你帮忙算算,销售单价定为多少?
四川地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小货车运送帐篷.计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次,两天恰好运完.
(1)求大、小货车原计划每辆每次各运送帐篷多少顶?
(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比原计划少运200m顶,每辆小货车每次比原计划少运300m顶,为了尽快将帐篷运送到灾区,大货车每天比原计划多跑 次,小货车每天比原计划多跑m次,一天恰好运送了帐篷14400顶,求m的值.
次,小货车每天比原计划多跑m次,一天恰好运送了帐篷14400顶,求m的值.
为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题: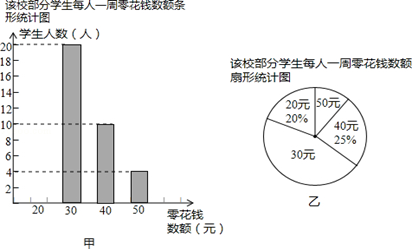
(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?补调查的学生每人一周零花钱数额的中位数是多少元?
(3)四川地震后,全校1000名学生每人自发地捐出一周零花钱的一半,以支援灾区建设.请估算全校学生共捐款多少元?
如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE=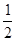 BC,连结DE,CF。
BC,连结DE,CF。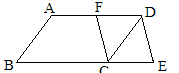
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
(1)计算:
(2)解方程:(2x-1)2=x(3x+2)-7
观察下列各式,请你找出规律回答以下问题:
2=2×1
2+4=6=2×3
2+4+6=12=3×4
2+4+6+8=20=4×5
......
计算:
(1)2+4+6+8+10+....+20=
(2)2+4+6+8+10+....+2×n=
(3)30+32+34+36+....+200=