如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
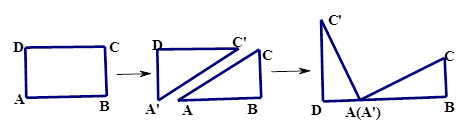
将矩形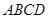 纸片沿对角线
纸片沿对角线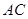 剪开,得
剪开,得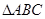 和
和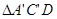 ,如图(1-1)所示.将
,如图(1-1)所示.将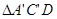 的顶点
的顶点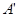 与点
与点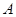 重合,并绕点
重合,并绕点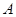 按逆时针方向旋转,使点
按逆时针方向旋转,使点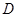 、
、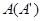 、
、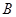 在同一条直线上,如图(1-2)所示.
在同一条直线上,如图(1-2)所示.观察图可知:与BC相等的线段是______,
 =_______;
=_______;
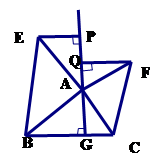
如图(2),
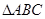 中,
中,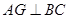 于点
于点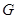 ,以
,以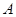 为直角顶点,分别以
为直角顶点,分别以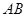 、
、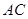 为直角边,向
为直角边,向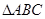 外作等腰
外作等腰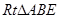 和等腰
和等腰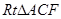 ,过点
,过点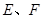 作射线
作射线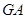 的垂线,垂足分别为
的垂线,垂足分别为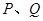 . 求证:
. 求证: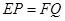 .
.
如图(3),
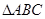 中,
中,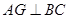 于点
于点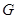 ,以
,以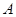 为直角顶点,分别以
为直角顶点,分别以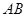 、
、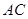 为直角边,向
为直角边,向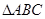 外作
外作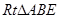 和
和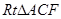 ,过点
,过点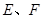 作射线
作射线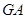 的垂线,垂足分别为
的垂线,垂足分别为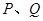 .若
.若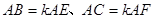 ,试探究
,试探究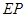 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.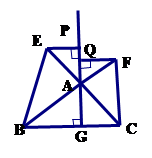
如图25,一次函数 的图象与反比例函数
的图象与反比例函数 的图象相交于A、B两点.
的图象相交于A、B两点.利用图中条件,求反比例函数和一次函数的解析式
根据图象写出使反比例函数的值大于一次函数的值的
 的取值范围 .
的取值范围 .
如图24,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9 m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2 m,又测得地面部分的影长(BC)为2.7 m,他测得的树高应为多少米?
初二(1)班的大课间活动丰富多彩,小文与小月进行跳绳比赛.在相同时间内,小文跳了180个,小月跳了210个,已知小月每分钟比小文多跳20个,问小月、小文每分钟各跳多少个?
如图22,在12×12的正方形网格中,△TAB 的顶点坐标T(1,1)、A(2,3)、B(4,2).以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1,并在位似中心的同侧,将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
在(1)中,若C(a,b)为线段AB上任意一点,写出变化后C的对应点
C′的坐标.