如图,已知点 在二次函数 的图象上,且 .
(1)若二次函数的图象经过点 .
①求这个二次函数的表达式;
②若 ,求顶点到 的距离;
(2)当 时,二次函数的最大值与最小值的差为 ,点 在对称轴的异侧,求 的取值范围.

如图,某小区有一长为30m,宽为20m的广场,图案如下,其中白色区域四周出口的宽度一样.小明在规定地点随意向图案内投掷小球,每球都能落在图案内,经过多次试验,发现落在黑色区域的概率是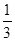 ,那么白色区域四周出口的宽度应是多少?
,那么白色区域四周出口的宽度应是多少?
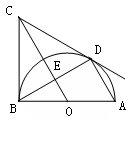
如图,AB是半圆O的直径,AD为弦,BC是半圆O的切线,OC∥AD,求证:CD是半圆O的切线
若BD=BC=6,求AD的长.
如图,在平面直角坐标系中,△ABC的三个顶点
坐标分别是A(2,3)、B(2,1)、C(3,2).
①判断△ABC的形状;②如果将△ABC沿着边AC旋转,求所得旋转体的全面积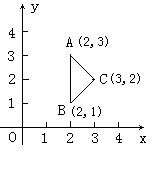
如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的格点上.
①在图甲中作出的四边形是中心对称图形但不是轴对称图形;
②在图乙中作出的四边形是轴对称图形但不是中心对称图形;
③在图丙中作出的四边形既是轴对称图形又是中心对称图形.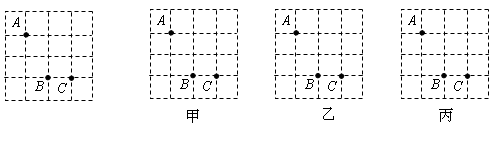
如图,已知:抛物线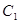 ,
,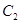 关于
关于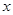 轴对称;抛物线
轴对称;抛物线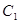 ,
,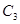 关于
关于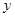 轴对称。
轴对称。
如果抛物线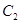 的解析式是
的解析式是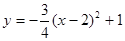 ,那么抛物线
,那么抛物线 的解析式
的解析式
是.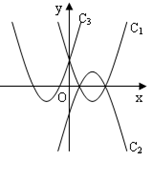
如图,在直角坐标系中,点 在
在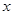 轴上,⊙
轴上,⊙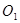 与
与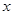 轴交于点
轴交于点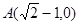 ,
,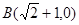 .直线
.直线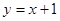 与坐标轴交于C 、D两点,直线在⊙
与坐标轴交于C 、D两点,直线在⊙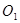 的左侧.
的左侧.求
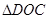 的面积;
的面积;当直线向右平移,第一次与⊙
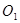 相切时,求直线的解析式.
相切时,求直线的解析式.