已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．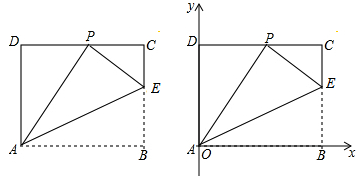
（1）如图，已知折痕与边BC交于点E，连结AP、EP、EA．求证：△ECP∽△PDA；
（2）若△ECP与△PDA的面积比为1：4，求边AB的长；
（3）在（2）的条件下以点A为坐标原点，AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，问在坐标平面内是否存在点M，使得以点A、B、E、M为顶点的四边形是平行四边形，若存在请直接写出点M的坐标；若不存在请说明理由。
“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技比赛．下图为我市某校2011年参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图：
（1）该校参加机器人、建模比赛的人数分别是人和人；
（2）该校参加科技比赛的总人数是人，电子百拼所在扇形的圆心角的度数是°，并把条形统计图补充完整；
（3）从全市中小学参加科技比赛选手中随机抽取80人，其中有32人获奖. 今年我市
中小学参加科技比赛人数共有2485人，请你估算今年参加科技比赛的获奖人数约是多少人?
如图所示，每一个小方格都是边长为1的单位正方形。△ABC的三个顶点都在格点上，以点O为坐标原点建立平面直角坐标系。
（1）画出△ABC先向左平移3个单位，再向下平移2个单位的△A1B1C1，并写出点B1的坐标；
（2）画出将△ABC绕点O顺时针旋转90°后的△A2B2C2，并求出点A旋转到A2所经过的路径长。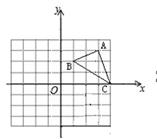
已知关于
的函数
的图像与坐标轴只有2个交点，求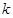
的值.
先化简，再求值：
，其中a=2－
计算：