某投资公司计划投资A，B两种金融产品，根据市场调查与预测，A-优题课

某投资公司计划投资A，B两种金融产品，根据市场调查与预测，A产品的利润与投资量成正比，其关系如图1，B产品的利润与投资量的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）

（1）分别将A，B两产品的利润表示为投资量的函数关系式；
（2）该公司已有10万元资金，并全部投入A，B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？

科目数学题型解答题难度中等

知识点：不定方程和方程组

某射手每次射击击中目标的概率是 $\frac{2}{3}$ ，且各次射击的结果互不影响。
（Ⅰ）假设这名射手射击5次，求恰有2次击中目标的概率
（Ⅱ）假设这名射手射击5次，求有3次连续击中目标。另外2次未击中目标的概率；
（Ⅲ）假设这名射手射击3次，每次射击，击中目标得1分，未击中目标得0分，在3次射击中，若有2次连续击中，而另外1次未击中，则额外加1分；若3次全击中，则额外加3分，记 $ξ$ 为射手射击3次后的总的分数，求 $ξ$ 的分布列。

已知函数 $f (x) = 2 \sqrt{3} \sin x \cos x + 2 \cos^{2} x - 1 (x \in R)$

（Ⅰ）求函数 $f (x)$ 的最小正周期及在区间 $[0, \frac{π}{2}]$ 上的最大值和最小值；
（Ⅱ）若 $f (x_{2}) = \frac{6}{5}, x_{0} \in [\frac{π}{4}, \frac{π}{2}]$ ，求 $\cos 2 x_{0}$ 的值。

设函数 $f (x) = |2 x - 4| + 1$

（Ⅰ）画出函数 $y = f (x)$ 的图像
（Ⅱ）若不等式 $f (x) \leq a x$ 的解集非空，求 $a$ 的取值范围.

已知直线 $C_{1} : {\begin{matrix} x = 1 + t \cos a \\ y = t \sin a \end{matrix}$ （ $t$ 为参数）， $C_{2} : {\begin{matrix} x = \cos θ \\ y = \sin θ \end{matrix}$ （ $θ$ 为参数），
（Ⅰ）当 $a = \frac{π}{3}$ 时，求 $C_{1_{}}$ 与 $C_{2}$ 的交点坐标；
（Ⅱ）过坐标原点 $O$ 做 $C_{1_{}}$ 的垂线，垂足为 $P$ ， $P$ 为 $O A$ 中点，当 $a$ 变化时，求 $P$ 点的轨迹的参数方程，并指出它是什么曲线.

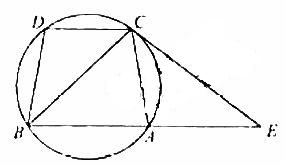
如图，已经圆上的弧 $\overset{⏜}{A C} = \overset{⏜}{B D}$ ，过 $C$ 点的圆切线与 $B A$ 的延长线交于 $E$ 点，证明：
（Ⅰ） $∠ A C E = ∠ B C D$ ；
（Ⅱ） $B C^{2} = B F \times C D$ .

试卷网试题网古诗词网作文网范文网