己知椭圆C：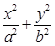
=1（a＞b＞0）的离心率为
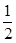，以原点为圆心，椭圆的短半轴为半径的圆与直线x-y+
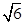=0相切，过点P（4，0）且不垂直于x轴直线，与椭圆C相交于A、B两点．
（1）求椭圆C的方程：
（2）求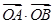
的取值范围；
（3）若B点关于x轴的对称点是E，证明：直线AE与x轴相交于定点．
(12分)某市中学生田径运动会总分获得冠、亚、季军的代表队人数如下表,大会组委会为使颁奖仪式有序进行,用分层抽样的方法从三个代表队中抽取16人在前排就座,其中亚军队有5人.
(1)求季军队中男运动员的人数(2)从前排就座的亚军队5人(3男2女)中随机抽取2人上台领奖请列出所有的基本事件,并求亚军队中有女生上台领奖的概率;
| 性别名次 |
冠军 |
亚军 |
季军 |
| 男生 |
30 |
30 |
 |
| 女生 |
30 |
20 |
30 |
(12分)抛物线的顶点在坐标原点,焦点在
轴的负半轴上,过点
作直线
与抛物线交于A,B两点,且满足
,
(1)求抛物线的方程
(2)当抛物线上的一动点P从A运动到B时,求
面积的的最大值．
(12分)在四棱锥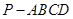
中,底面ABCD是边长为1的正方形,
平面ABCD,PA=AB,M,N分别为PB,AC的中点,
（１）求证:MN //平面PAD（２）求点B到平面AMN的距离
(12分)已知数列
是公差不为零的等差数列,
且
成等比数列
（１）求数列的通项公式（２）求数列
的前
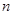项和
(10分)已知函数
（１）求
的最小正周期和值域（２）求的单调递增区间