11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题:小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远?
(本题10分)解下列一元二次方程:
(1)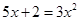 (用公式法解);(2)
(用公式法解);(2)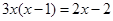 .
.
如图1,在平面直角坐标系中,抛物线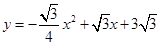 交
交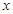 轴于A,B两点(点A在点B的左侧),交
轴于A,B两点(点A在点B的左侧),交 轴于点W,顶点为C,抛物线的对称轴与
轴于点W,顶点为C,抛物线的对称轴与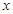 轴的交点为D。
轴的交点为D。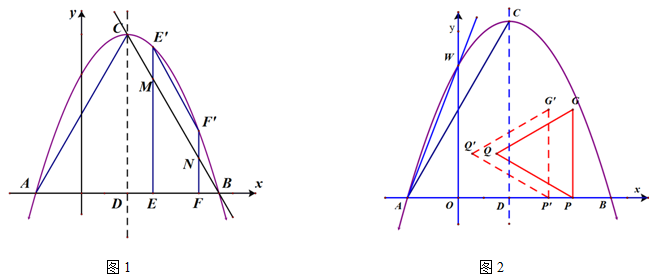
(1)求直线BC的解析式;
(2)点E(m,0),F(m+2,0)为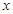 轴上两点,其中
轴上两点,其中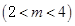 ,
,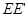 ,
,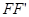 分别垂直于
分别垂直于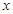 轴,交抛物线与点
轴,交抛物线与点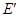 ,
,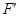 ,交BC于点M,N,当
,交BC于点M,N,当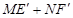 的值最大时,在
的值最大时,在 轴上找一点R,使
轴上找一点R,使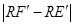 的值最大,请求出R点的坐标及
的值最大,请求出R点的坐标及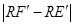 的最大值;
的最大值;
(3)如图2,已知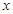 轴上一点
轴上一点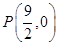 ,现以P为顶点,
,现以P为顶点,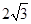 为边长在
为边长在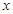 轴上方作等边三角形QPG,使GP⊥
轴上方作等边三角形QPG,使GP⊥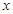 轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为
轴,现将△QPG沿PA方向以每秒1个单位长度的速度平移,当点P到达点A时停止,记平移后的△QPG为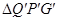 ,设
,设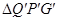 与△ADC的重叠部分面积为s,当点
与△ADC的重叠部分面积为s,当点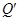 到
到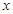 轴的距离与点
轴的距离与点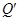 到直线AW的距离相等时,求s的值。
到直线AW的距离相等时,求s的值。
如图1,在△ABC中,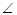 ACB=90°,
ACB=90°,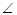 BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,点F是BD的中点.DH⊥AC,垂足为H,连接EF,HF。
BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的线段,两垂线交于点D,连接DB,点F是BD的中点.DH⊥AC,垂足为H,连接EF,HF。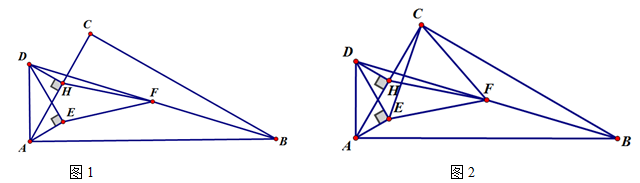
(1)如图1,若点H是AC的中点,AC=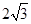 ,求AB,BD的长。
,求AB,BD的长。
(2)如图1,求证:HF=EF。
(3)如图2,连接CF,CE,猜想:△CEF是否是等边三角形?若是,请证明;若不是,请说明理由。
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角 ,渔船N在俯角
,渔船N在俯角 ,已知MN所在直线与PC所在直线垂直,垂足为点E,且PE长为30米.
,已知MN所在直线与PC所在直线垂直,垂足为点E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度 .为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度为
.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度为 ,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
,施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据: )
)
为贯彻政府报告中“全民创新,万众创业”的精神,某镇对辖区内所有的小微企业按年利润 (万元)的多少分为以下四个类型:A类(
(万元)的多少分为以下四个类型:A类( ),B类(
),B类( ),C类(
),C类( ),D类(
),D类( ),该镇政府对辖区对辖区内所有的小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
),该镇政府对辖区对辖区内所有的小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
(1)该镇本次统计的小微企业总个数是,扇形统计图中B类所对应扇形圆心角的度数为度,请补全条形统计图;
(2)为进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会,计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中2个来自高新区,另2个来自开发区,请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率。