设全集为R, ,
, ,
,
 .
.
(1)求 及
及
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线,
(单位:小时)之间近似满足如图所示的曲线,
(1)写出第一次服药后 与
与 之间的函数关系式;
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到 ,参考数据:
,参考数据: )
)
已知函数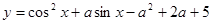 有最大值
有最大值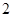 ,求实数
,求实数 的值.
的值.
已知函数 (其中
(其中 )的图像过点
)的图像过点 ,且其相邻两条对称轴之间的距离为
,且其相邻两条对称轴之间的距离为 ,
,
(1)求实数 的值及
的值及 的单调递增区间;
的单调递增区间;
(2)若 ,求
,求 的值域.
的值域.
已知 为第三象限角,
为第三象限角, ,
,
(1)化简 ;
;
(2)若 ,求
,求 的值.
的值.
设全集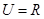 ,已知函数
,已知函数 的定义域为集合
的定义域为集合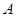 ,函数
,函数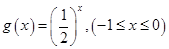 的值域为集合
的值域为集合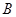 ,
,
(1)求 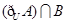 ;
;
(2)若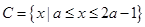 且
且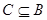 ,求实数
,求实数 的取值范围.
的取值范围.