已知定义在 上的函数
上的函数 同时满足下列三个条件:①
同时满足下列三个条件:① ;②对任意
;②对任意 都有
都有 ;③当
;③当 时,
时, .
.
(1)求 、
、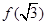 的值;
的值;
(2)证明:函数 在
在 上为减函数;
上为减函数;
(3)解关于 的不等式
的不等式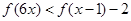 .
.
如图,抛物线 点 在抛物线 上,过 作 的切线,切点为 ( 为原点 时, 重合于 ),当 时,切线 的斜率为 .
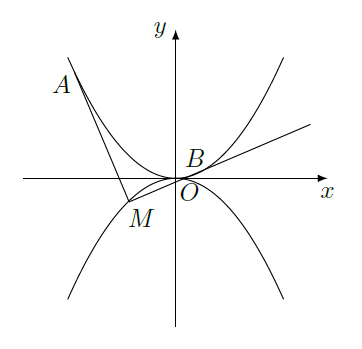
(I)求
的值;
(II)当
在
上运动时,求线段
中点
的轨迹方程(
重合于
时,中点为
).
现有6道题,其中4道甲类题,2道乙类题,张同学从中任取3道题解答.试求
(I)所取的2道题都是甲类题的概率;
(II)所取的2道题不是同一类题的概率.
如图, 是圆 的直径, 垂直圆 所在的平面, 是圆 上的点.
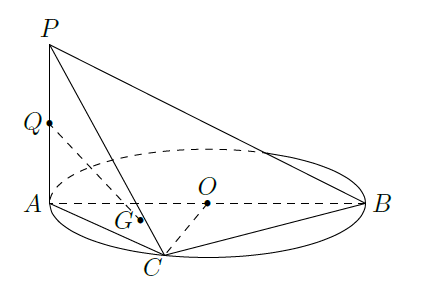
(I)求证:
(II)设
设向量
(I)若 ;
(II)设函数
定义区间 ,
,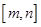 ,
, ,
, 的长度均为
的长度均为 ,其中
,其中 .
.
(1)求关于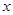 的不等式
的不等式 的解集构成的区间的长度;
的解集构成的区间的长度;
(2)若关于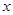 的不等式
的不等式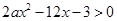 的解集构成的区间的长度为
的解集构成的区间的长度为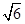 ,求实数
,求实数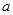 的值;
的值;
(3)已知关于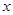 的不等式
的不等式 ,
, 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过 ,求实数
,求实数 的取值范围.
的取值范围.