(本小题满分13分)设F1,F2分别是椭圆 的左右焦点.
的左右焦点.
(1)若P是该椭圆上的一个动点,求 的最大值和最小值.
的最大值和最小值.
(2)是否存在经过点A(5,0)的直线l与椭圆交于不同的两点C,D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: ,
, ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(Ⅰ)求分数在 内的频率;
内的频率;
(Ⅱ)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分;
(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数.不低于90分的概率.
酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
依据上述材料回答下列问题:
(1)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(2)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率.(酒后驾车的人用大写字母如 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如 表示)
表示)
设命题p: ;命题q:
;命题q:  ,若
,若 是
是 的必要不充分条件,
的必要不充分条件,
(1)p是q的什么条件?
(2)求实数a的取值范围.
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为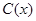 ,当年产量不足80千件时,
,当年产量不足80千件时,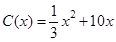 (万元)。当年产量不小于80千件时,
(万元)。当年产量不小于80千件时, (万元)。每件商品售价为0.05万元。通过市场分析,该厂生产的商品能全部售完。
(万元)。每件商品售价为0.05万元。通过市场分析,该厂生产的商品能全部售完。
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
已知各项均为正数的数列 前n项和为
前n项和为 ,首项为
,首项为 ,且
,且 成等差数列。
成等差数列。
(1)求数列 的通项公式;
的通项公式;
(2)若 ,设
,设 ,求数列
,求数列 的前n项和
的前n项和 .
.