某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段：
，
，…， 
后得到如下频率分布直方图．
（Ⅰ）求分数在
内的频率；
（Ⅱ）根据频率分布直方图，估计该校高二年级学生期中考试政治成绩的平均分；
（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数．不低于90分的概率．
画出下列函数的图象：
(1)y＝x2－2x 
；
(2)f(x)＝
；
(3)y＝x|2－x|.
画出下列函数的图象．
(1)y＝2x－1，x∈Z，|x|≤2；
(2)y＝2x2－4x－3(0≤x<3)；
(3)y＝
(lgx＋|lgx|)．
已知函数
和函数
，其中
为参数，且满足
.
（1）若
，写出函数
的单调区间（无需证明）；
（2）若方程
在
上有唯一解，求实数的取值范围；
（3）若对任意
，存在
，使得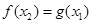
成立，求实数的取值范围.
修建一个面积为
平方米的矩形场地的围墙，要求在前面墙的正中间留一个宽度为2米的出入口，后面墙长度不超过20米.已知后面墙的造价为每米45元，其他墙的造价为每米180元，设后面墙长度为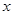
米，修建此矩形场地围墙的总费用为
元.
（1）求的表达式；
（2）试确定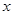，使修建此矩形场地围墙的总费用最小，并求出最小总费用.
已知函数
的部分图像如图所示.
（1）求
的值；
（2）求函数
的单调递增区间.