酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
依据上述材料回答下列问题:
(1)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(2)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率.(酒后驾车的人用大写字母如 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如 表示)
表示)
选修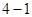 :几何证明选讲
:几何证明选讲
如图,已知圆 的两弦
的两弦 和
和 相交于点
相交于点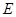 ,
, 是圆
是圆 的切线,
的切线, 为切点,
为切点, .求证:
.求证:
(Ⅰ) ;
;
(Ⅱ) ∥
∥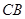 .
.
已知函数 ;(取
;(取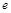 为
为 ,取
,取 为
为 ,取
,取 )
)
(Ⅰ)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(Ⅱ)若 有两个零点
有两个零点 ,求证:
,求证: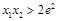 .
.
已知椭圆 :
: 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 与以椭圆
与以椭圆 的右焦点为圆心,以
的右焦点为圆心,以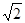
 为半径的圆相切.
为半径的圆相切.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点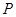 和
和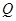 ,且原点
,且原点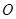 总在以
总在以 为直径的圆的内部,求实数
为直径的圆的内部,求实数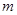 的取值范围.
的取值范围.
如图,四棱锥中, ∥,, ,若
,若 ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角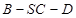 的余弦值.
的余弦值.
根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在 为优秀,人类可正常活动.某市环保局对该市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,人类可正常活动.某市环保局对该市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为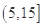 ,
, ,
, ,
, ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.
(Ⅰ)求 的值,并根据样本数据,试估计这一年度的空气质量指数的平均值;
的值,并根据样本数据,试估计这一年度的空气质量指数的平均值;
(Ⅱ)如果空气质量指数不超过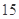 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.