已知函数 ;(取
;(取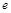 为
为 ,取
,取 为
为 ,取
,取 )
)
(Ⅰ)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(Ⅱ)若 有两个零点
有两个零点 ,求证:
,求证: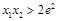 .
.
(本小题12分)在△ABC中,A,B,C所对的边分别为a,b,c,向量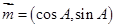 ,向量
,向量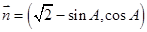 .若
.若 .
.
(1)求角A的大小;
(2)若△ABC外接圆的半径为2,b=2,求边c的长.
(本小题12分)已知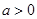 ,命题
,命题 :
: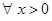 ,
, 恒成立,命题
恒成立,命题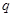 :
: ,直线
,直线 与椭圆
与椭圆 有公共点,求使得
有公共点,求使得 为真命题,
为真命题, 为假命题的实数
为假命题的实数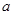 的取值范围.
的取值范围.
(本小题10分)已知命题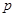 :方程
:方程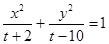 表示双曲线;命题
表示双曲线;命题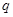 :
: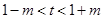 (
(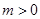 ),
),
若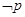 是
是 的充分非必要条件,试求实数
的充分非必要条件,试求实数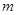 的取值范围.
的取值范围.
(本小题满分12分)设数列 的前
的前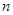 项和为
项和为 ,数列
,数列 的前
的前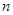 项和为
项和为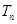 ,且满足
,且满足 .
.
(1)求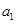 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)记  ,求证:
,求证: .
.
(本小题满分12分)设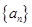 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且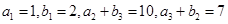 .
.
(1)求数列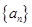 ,
, 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为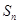 ,记
,记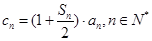 ,求数列
,求数列 的前
的前 项和
项和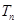 .
.