(文)我国是世界上严重缺水的国家之一,城市缺水问题较为突出。某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准。为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况。现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如下图表: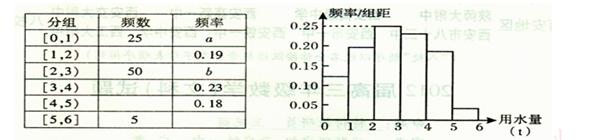
(1)分别求出n,a,b的值;
(2)若从样本中月均用水量在[5,6](单位:t)的5位居民中任选2人作进一步的调查研究,求月均用水量最多的居民被选中的频率(5位居民的月均用水量均不相等。)
根据空气质量指数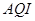 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
 (数值) (数值) |
 |
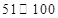 |
 |
 |
 |
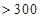 |
| 空气质量级别 |
一级 |
二级 |
三级 |
四级 |
五级 |
六级 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
| 空气质量类别颜色 |
绿色 |
黄色 |
橙色 |
红色 |
紫色 |
褐红色 |
某市 年
年 月
月 日—
日—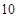 月
月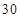 日,对空气质量指数
日,对空气质量指数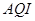 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图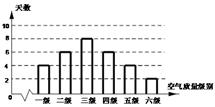
(1)估计该城市本月(按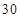 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率;
(2)在空气质量类别颜色为紫色和褐红色的数据中任取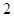 个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
设数列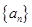 是公比为正数的等比数列,
是公比为正数的等比数列,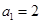 ,
,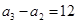 .
.
(1)求数列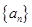 的通项公式;
的通项公式;
(2)设数列 是首项为
是首项为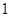 ,公差为
,公差为 的等差数列,求数列
的等差数列,求数列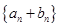 的前
的前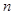 项和
项和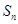 .
.
已知 ,函数
,函数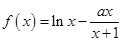 .
.
(1)当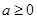 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)当 有两个极值点(设为
有两个极值点(设为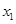 和
和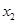 )时,求证:
)时,求证: .
.
如图,已知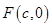 是椭圆
是椭圆 的右焦点;圆
的右焦点;圆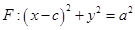 与
与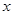 轴交于
轴交于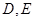 两点,其中
两点,其中 是椭圆
是椭圆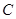 的左焦点.
的左焦点.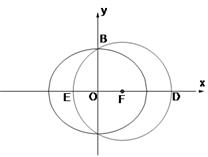
(1)求椭圆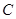 的离心率;
的离心率;
(2)设圆 与
与 轴的正半轴的交点为
轴的正半轴的交点为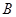 ,点
,点 是点
是点 关于
关于 轴的对称点,试判断直线
轴的对称点,试判断直线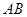 与圆
与圆 的位置关系;
的位置关系;
(3)设直线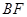 与圆
与圆 交于另一点
交于另一点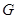 ,若
,若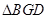 的面积为
的面积为 ,求椭圆
,求椭圆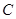 的标准方程.
的标准方程.
如图,已知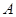 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且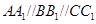 ,
,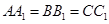 .
.
(1)求证:平面 //平面
//平面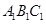 ;
;
(2)若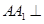 平面
平面 ,且
,且 ,
, ,
,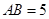 ,求证:
,求证: 平面
平面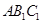 ;
;
(3)在(2)的条件下,求二面角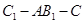 的余弦值.
的余弦值.