已知椭圆C的中心在原点,以坐标轴为对称轴,且经过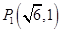 ,
,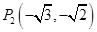 两点.
两点.
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)过点 作椭圆的弦
作椭圆的弦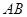 ,使点
,使点 为弦
为弦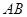 的中点,求弦
的中点,求弦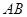 的长.
的长.
(本小题满分12分)
设O为坐标原点,点P的坐标
(I)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最
 大值,并求事件“|OP|取到最大值”的概率;
大值,并求事件“|OP|取到最大值”的概率;
(II)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
(本小题满分12分)
在
(1)求角C的大小;
(2)若AB边的长为 ,求BC边的长.
,求BC边的长.
(本小题满分12分)
已知函数
(1)确定 上的单调性;
上的单调性;
(2)设 在(0,2)上有极值,求
在(0,2)上有极值,求 的取值范围。
的取值范围。
(本小题满分12分)
已知半圆 ,动圆与此半圆相切且与
,动圆与此半圆相切且与 轴相切。
轴相切。
(1)求动圆圆心的轨迹,并画出其轨迹图形;
(2)是否存在斜率为 的直线
的直线 ,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足
,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足 。若存在,求出
。若存在,求出 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。