如图,现要在边长为100m的正方形ABCD内建一个交通“环岛”.以正方形的四个顶点为圆心在四个角分别建半径为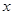 m(
m(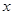 不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为
不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地,为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均不小于10m.
的圆形草地,为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均不小于10m.
(1)求x的取值范围(运算中 取1.4);
取1.4);
(2)若中间草地的造价为 ,四个花坛的造价为
,四个花坛的造价为 ,其余区域造价为
,其余区域造价为 ,当x取何值时,“环岛”的整体造价最低?
,当x取何值时,“环岛”的整体造价最低?
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组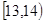 ,第二组
,第二组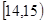 ……第五组
……第五组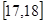 如图是按上述分组方法得到的频率分布直方图.
如图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于等于14秒且小于16秒规定为良好,求该班在这次百米测试中成绩为良好的人数。
(2)设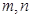 表示该班两个学生的百米测试成绩,已知
表示该班两个学生的百米测试成绩,已知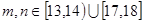 求事件“
求事件“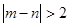 ”的概率。
”的概率。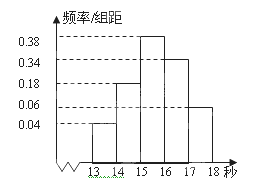
已知以角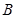 为钝角的
为钝角的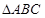 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c, ,且
,且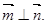
(1)求角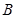 的大小;
的大小;
(2)求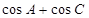 的取值范围.
的取值范围.
(本题14分)已知定义域为R的函数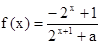 是奇函数。(1)求a的值;(2)用定义判断该函数的单调性(3)若对任意的
是奇函数。(1)求a的值;(2)用定义判断该函数的单调性(3)若对任意的 ,不等式
,不等式 恒成立,求k的取值范围;
恒成立,求k的取值范围;
(本题14分)如图,在棱长为1的正方体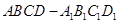 中,E,P分别是侧棱B1C1,
中,E,P分别是侧棱B1C1, 上的中点
上的中点
(1)求证:A1E//平面D1AP
(2)求直线AP与平面 所成角的正切值
所成角的正切值
(本题14分)已知与圆C: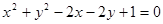 相切的直线
相切的直线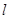 交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).
交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).
(1)求b的值;
(2)求△ABC的外接圆方程。