核聚变能是一种具有经济性能优越、安全可靠、无环境污染等优势的新能源。近年来,受控核聚变的科学可行性已得到验证,目前正在突破关键技术,最终将建成商用核聚变电站。一种常见的核聚变反应是由氢的同位素氘(又叫重氢)和氚(又叫超重氢)聚合成氦,并释放一个中子。若已知氘原子的质量为2.0141u,氚原子的质量为3.0160u,氦原子的质量为4.0026u,中子的质量为1.0087u,1u=1.66×10-27kg。
(1)写出氘和氚聚合的反应方程。
(2)试计算这个核反应释放出来的能量。
(3)若建一座功率为3.0×105kw的核聚变电站,假设聚变所产生的能量有一半变成了电能,每年要消耗多少氘的质量?(一年按3.2×107s计算,光速c=3.00×108m/s,结果取二位有效数字)
如图,绝缘的光滑水平面上,紧靠左边的竖直墙面固定有一水平弹簧枪,某时刻枪发射出一颗质量为m、速度为υ0,不带电的子弹P,子弹水平射入停在同一水平面上B点处的小球Q而未穿出。小球Q带正电,电量为q、质量为3m,接着两者一起向前运动,从C点进入一正交的匀强电场和匀强磁场区域,电场方向竖直向上,磁场方向垂直纸面向里。小球进入电磁场后在竖直平面内做匀速圆周运动,最后小球飞出电磁场刚好落到水平面上的B点,CC′是磁场和电场的共同边界线,已知 ,不计空气阻力,重力加速度为g,求:
,不计空气阻力,重力加速度为g,求: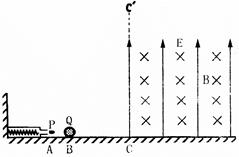
匀强磁场的磁感应强度的大小。
小球从B点出发再落回到B点所经历的时间为多少?
如图所示,一边长L=0.2m,质量m1=0.5kg,电阻R=0.1Ω的正方形导体线框abcd,与一质量为m2=2kg的物块通过轻质细线跨过两定滑轮相连。起初ad边距磁场下边界为d1=0.8m,磁感应强度B=2.5T,磁场宽度d2=0.3m,物块放在倾角θ=530的斜面上,物块与斜面间的动摩擦因数 =0.5。现将物块由静止释放,经一段时间后发现当ad边从磁场上边缘穿出时,线框恰好做匀速运动。(g取10m/s2,sin530=0.8,cos530=0.6)求:
=0.5。现将物块由静止释放,经一段时间后发现当ad边从磁场上边缘穿出时,线框恰好做匀速运动。(g取10m/s2,sin530=0.8,cos530=0.6)求:
线框ad边从磁场上边缘穿出时速度的大小?
线框刚刚全部进入磁场时动能的大小?
整个运动过程线框中产生的焦耳热为多少?
如图所示,在倾角为 的光滑斜面顶端有一质点
的光滑斜面顶端有一质点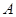 自静止开始自由下滑,同时另一质点
自静止开始自由下滑,同时另一质点 自静止开始由斜面底端向左以恒定加速度
自静止开始由斜面底端向左以恒定加速度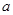 沿光滑水平面运动,
沿光滑水平面运动,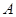 滑下后能沿斜面底部的光滑小圆弧平稳地朝
滑下后能沿斜面底部的光滑小圆弧平稳地朝 追去,为使
追去,为使 能追上
能追上 ,
, 的加速度最大值是多少?
的加速度最大值是多少?
如图所示,某货场需将质量m1=100 kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物由轨道顶端无初速度滑下,轨道半径R=1.8 m.地面上紧靠轨道依次排放两块完全相同的木板A、B,长度均为l=2 m,质量均为m2=100 kg,木板上表面与轨道末端相切.货物与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ2=0.2.(最大静摩擦力与滑动摩擦力大小相等,取g=10 m/s2)
(1)求货物到达圆轨道末端时对轨道的压力大小和方向。
(2)若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件.
(3)若μ1=0.5,求货物滑到木板A末端时的速度和在木板A上运动的时间.
如图所示,在光滑的水平面上停着一辆小车,小车平台的上表面是粗糙的。它靠在光滑的水平桌面旁并与桌面等高。现在有一个质量为m = 2kg的物体C以速度v0 = 10m/s沿水平桌面向右运动,滑过小车平台后从A点离开,恰能落在小车前端的B点。已知小车总质量为M=5kg,O点在A点的正下方,OA=0.8m,OB=1.2m,物体与小车摩擦系数µ = 0.2,g取10m/s2。求:
(1)物体刚离开平台时,小车获得的速度大小。
(2)物体在小车平台上运动的过程中,小车对地发生多大的位移。