如甲图所示,长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处平滑连接,有一质量为2kg的滑块,从A处由静止开始受水平向右的力F作用,F与位移x的关系按乙图所示规律变化,滑块与AB和BC间的动摩擦因数均为0.5,重力加速度g取l0m/s2。求:
(1)滑块第一次到达B处时的速度大小;
(2)不计滑块在B处的速率变化,滑块到达B点时撤去力F,滑块冲上斜面,则滑块最终静止的位置与B点的距离多大。(sin37°=0.6)
在光滑的水平面上,一质量为mA=0.1kg的小球A,以8 m/s的初速度向右运动,与质量为mB=0.2kg的静止小球B发生弹性正碰。碰后小球B滑向与水平面相切、半径为R=0.5m的竖直放置的光滑半圆形轨道,且恰好能通过最高点N后水平抛出。g=10m/s2。求: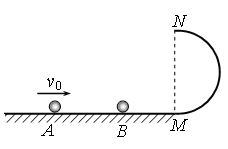
(1) 碰撞后小球B的速度大小;
(2) 小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量;
(3) 碰撞过程中系统的机械能损失。
有频率相同、振动方向相同的两个声源S1和S2,如图所示.一人站在声源北方的A点,此人此时听到的声音很响,这个人向东慢慢移动,声音逐渐减弱,到B点时几乎听不到声音,测得A、B间距离为1.5 m.则: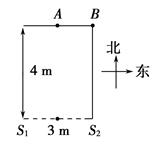
①S1、S2声波的波长λ为多少?
②若此人由B点再向正南方向移动,声音逐渐变响,那么,此人沿正南方向至少走多远,声音又变得很响?
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1 =" 0.40" T,方向垂直纸面向里,电场强度E = 2.0×105 V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域(图中未画出),磁感应强度B2 =" 0.25" T。一束带电量q = 8.0×10-19 C,质量m = 8.0×10-26 kg的正离子从P点射入平行板间,不计重力,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射向三角形磁场区,离子通过x轴时的速度方向与x轴正方向夹角为60°。则: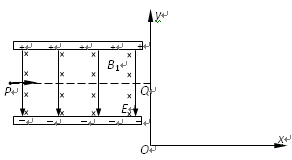
(1)离子运动的速度为多大?
(2)若正三角形区域内的匀强磁场方向垂直纸面向外,离子在磁场中运动的时间是多少?
(3)若正三角形区域内的匀强磁场方向垂直纸面向里,正三角形磁场区域的最小边长为多少?
(4)第(3)问中离子出磁场后经多长时间到达X轴?
如图,足够长斜面倾角θ=30°,斜面上OA段光滑,A点下方粗糙且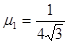 ,水平面上足够长OB段粗糙且μ2=0.5,B点右侧水平面光滑。OB之间有与水平方向β(β已知)斜向右上方的匀强电场E=
,水平面上足够长OB段粗糙且μ2=0.5,B点右侧水平面光滑。OB之间有与水平方向β(β已知)斜向右上方的匀强电场E=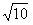 ×105V/m。可视为质点的小物体C、D质量分别为mC=4kg,mD=1kg,D带电q= +1×10-4C,用轻质细线通过光滑滑轮连在一起,分别放在斜面及水平面上的P和Q点由静止释放,B、Q间距离d=1m,A、P间距离为2d,细绳与滑轮之间的摩擦不计。(sinβ=
×105V/m。可视为质点的小物体C、D质量分别为mC=4kg,mD=1kg,D带电q= +1×10-4C,用轻质细线通过光滑滑轮连在一起,分别放在斜面及水平面上的P和Q点由静止释放,B、Q间距离d=1m,A、P间距离为2d,细绳与滑轮之间的摩擦不计。(sinβ=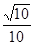 ,cosβ=
,cosβ=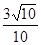 ,g=10m/s2),求:
,g=10m/s2),求: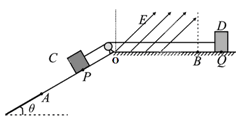
(1)物体C第一次运动到A点时速度;
(2)物块D运动过程中电势能变化量的最大值。