两个重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车.已知该火车每日往返的次数 是车头每次拖挂车厢节数
是车头每次拖挂车厢节数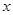 的一次函数.若车头拖挂
的一次函数.若车头拖挂 节车厢,则每日能往返
节车厢,则每日能往返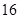 次;若车头每次拖挂
次;若车头每次拖挂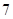 节车厢,则每日能往返
节车厢,则每日能往返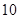 次.
次.
(1)求此一次函数;
(2)求这列火车每天运营的车厢总节数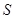 关于
关于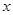 的函数;
的函数;
(3)若每节车厢能载旅客 人,求每次车头拖挂多少节车厢可使每天运送的旅客人数最多,并求出每天最多运送旅客人数.
人,求每次车头拖挂多少节车厢可使每天运送的旅客人数最多,并求出每天最多运送旅客人数.
选修4—5:不等式选讲.
设函数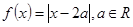 .
.
(1)若不等式 的解集为
的解集为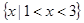 ,求
,求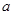 的值;
的值;
(2)若存在 ,使
,使 ,求
,求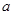 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程选讲.
已知直线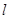 的参数方程为
的参数方程为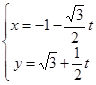 (
(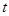 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,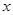 轴的正半轴为极轴建立极
轴的正半轴为极轴建立极
坐标系,圆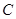 的极坐标方程为
的极坐标方程为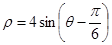 .
.
(1)求圆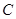 的直角坐标方程;
的直角坐标方程;
(2)若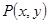 是直线
是直线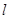 与圆面
与圆面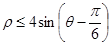 的公共点,求
的公共点,求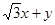 的取值范围.
的取值范围.
选修4—1:几何证明选讲.
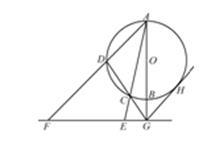
如图,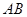 是圆
是圆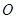 的直径,
的直径,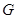 是
是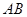 延长线上的一点,
延长线上的一点,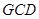 是圆
是圆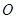 的割线,过点
的割线,过点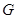 作
作 的垂线,交直线
的垂线,交直线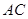 于点
于点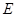 ,交直线
,交直线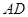 于点
于点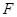 ,过点
,过点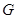 作圆
作圆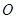 的切线,切点为
的切线,切点为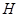 .
.
(1)求证: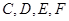 四点共圆;
四点共圆;
(2)若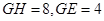 ,求
,求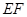 的长.
的长.
已知函数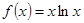 .
.
(1)求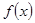 的单调区间和极值;
的单调区间和极值;
(2)设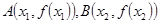 ,且
,且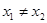 ,证明:
,证明: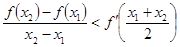 .
.
已知双曲线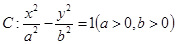 的焦距为
的焦距为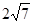 ,其一条渐近线的倾斜角为
,其一条渐近线的倾斜角为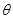 ,且
,且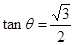 ,以双曲线
,以双曲线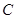 的实轴为长轴,虚轴为短轴的椭圆为
的实轴为长轴,虚轴为短轴的椭圆为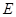 .
.
(1)求椭圆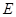 的方程;
的方程;
(2)设点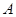 是椭圆
是椭圆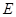 的左顶点,
的左顶点,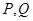 为椭圆
为椭圆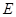 上异于点
上异于点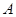 的两动点,若直线
的两动点,若直线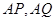 的斜率之积为
的斜率之积为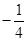 ,问直线
,问直线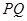 是否恒过定点?若横过定点,求出该点坐标;若不横过定点,说明理由.
是否恒过定点?若横过定点,求出该点坐标;若不横过定点,说明理由.