在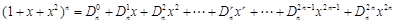
的展开式中，把
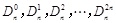叫做三项式系数．
（1）当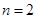
时，写出三项式系数
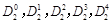的值；
（2）类比二项式系数性质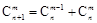
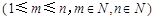，给出一个关于三项式系数
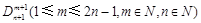的相似性质，并予以证明；
（3）求
的值．
（本小题满分14分）已知函数
（I）求曲线
处的切线方程；（Ⅱ）求证函数
在区间[0，1]上存在唯一的极值点，并用二分法求函数取得极值时相应x的近似值（误差不超过0.2）；（参考数据e≈2.7，
≈1.6，e0.3≈1.3）
（III）当
试求实数
的取值范围。
（本小题满分12分）工厂生产某种产品，次品率p与日产量x（万件）间的关系为
已知每生产1件合格产品盈利3元，每出现重件次品亏损1.5元． （I）将日盈利额y（万元）表示为日产量
（万件）的函数； （Ⅱ）为使日盈利额最大，日产量应为多少万件?（注：次品率=
×100％）
（本小题满分12分）已知等差数列{an}的首项
，前n项和为Sn，且S4+a2=2S3；等比数列{bn}满足b1=a2，b2=a4（Ⅰ）求证：数列{bn}中的每一项都是数列{an}中的项；
（Ⅱ）若a1=2，设
，求数列{cn}的前n项的和Tn
（Ⅲ）在（Ⅱ）的条件下，若有
的最大值．
（本小题满分12分）
如图1，矩形ABCD中，AB=2AD=2a，E为DC的中点，现将△ADE沿AE折起，使平面ADE⊥平面ABCE，如图2．（I）求二面角A—BC—D的正切值；
|
（Ⅱ）求证：AD⊥平面BDE．
（本小题满分12分）向量a=（sinωx+cosωx，1），b=（f（x），simωx），其中0<ω<l，且a∥b．将f（x）的图象沿x轴向左平移
个单位，沿y轴向下平移
个单位，得到g（x）的图象，已知g（x）的图象关于（，0）对称（I）求ω的值； （Ⅱ）求g（x）在[0，4π]上的单调递增区间．
