已知:如图A,△ABC各角的平分线AD,BE,CF交于点O.
(1)试说明∠BOC=90°+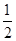 ∠BAC;
∠BAC;
(2)如图B,过点O作OG⊥BC于G,试判断∠BOD与∠COG的大小关系(大于,小于或等于),并说明理由.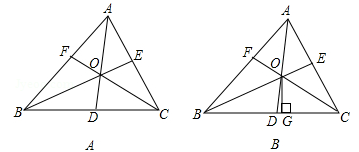
有20筐白菜,以每筐25千克为标准,超过千克数记为正数,不足的千克数记为负数,记录如表:
| 与标准质量的差值(单位:千克) |
-3 |
-2 |
-1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
4 |
6 |
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
某轮船顺水航行3小时,逆水航行1.5小时,已知轮船在静水中的速度是m千米/小时,水流速度是n千米/小时,求轮船共航行多少千米?
已知|x-2|+(y+1)2=0.
(1)求x、y的值;
(2)求-x3+y4的值.
化简求值:5(x2y-3x)-2(x-2x2y)+20x,其中x=-2,y=- .
.
计算:
(1)8a+2b+(5a-b)
(2)-x+(2x-2)-(3x+5)
(3)5x2-[x2+(5x2-2x)-2(x2-3x)].