已知:如图,以 的边
的边 为直径的
为直径的 交边
交边 于点
于点 ,且过 点
,且过 点 的切线
的切线 平分边
平分边 .
.

(1)求证: 是
是 的切线;
的切线;
(2)当 满足什么条件时,以点
满足什么条件时,以点 、
、 、
、 、
、 为顶点的四边形是平行四边形?请说明理由.
为顶点的四边形是平行四边形?请说明理由.
在平面直角坐标系中,二次函数 的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.
(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.
甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;
乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;
丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.
某仓库有甲种货物360吨,乙种货物290吨,计划用A、B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为x辆,运输这批货物的总运费为y万元,试写出y与x的关系表达式;
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案?请设计出来;
(3)试说明哪种方案总运费最少?最少运费是多少万元?
自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题: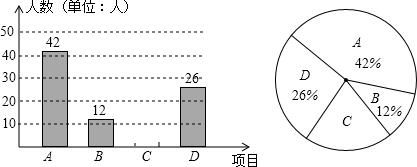
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.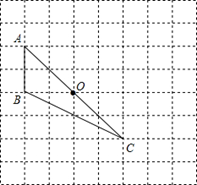
(1)将△ABC绕点O顺时针旋转90°后,得到△A1B1C1.在网格中画出△A1B1C1;
(2)求线段OA在旋转过程中扫过的图形面积;(结果保留π)
(3)求∠BCC1的正切值.