△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上,BC=30,AD=20.求这个正方形的边长.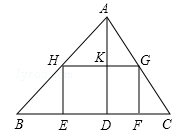
(本题8分)在梯形ABCD中,AD//BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.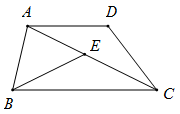
(1)求证:△DAC≌△ECB;
(2)若CA平分∠BCD,且AD=3,求BE的长.
(本题8分)已知二次函数 的图象经过点A(2, -3),B(-1,12).
的图象经过点A(2, -3),B(-1,12).
(1)求这个二次函数的解析式;
(2)求这个图象的顶点坐标和对称轴
(本题8分)
(1)计算: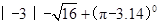 ;
;
(2)解不等式: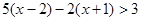
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式;
(3)当x为何值时,△HDE为等腰三角形?
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[50°, ]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线BC′所夹的锐角为度;
]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线BC′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ 和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ 和n的值.